
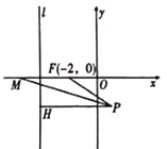
【题目】如图,在平面直角坐标系中,已知点![]() ,直线
,直线![]() ,过动点
,过动点![]() 作
作![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,且
,且![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作两条直线,分别交曲线
作两条直线,分别交曲线![]() 于
于![]() 两点(异于
两点(异于![]() 点).当直线
点).当直线![]() 的斜率之和为2时,直线
的斜率之和为2时,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
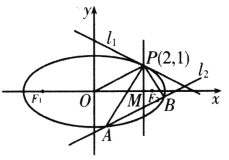
【题目】已知椭圆![]() 过点
过点![]() ,
,![]() 分别为椭圆C的左、右焦点且
分别为椭圆C的左、右焦点且![]() .
.
(1)求椭圆C的方程;
(2)过P点的直线![]() 与椭圆C有且只有一个公共点,直线
与椭圆C有且只有一个公共点,直线![]() 平行于OP(O为原点),且与椭圆C交于两点A、B,与直线
平行于OP(O为原点),且与椭圆C交于两点A、B,与直线![]() 交于点M(M介于A、B两点之间).
交于点M(M介于A、B两点之间).
(i)当![]() 面积最大时,求
面积最大时,求![]() 的方程;
的方程;
(ii)求证:![]() ,并判断
,并判断![]() ,
,![]() 的斜率是否可以按某种顺序构成等比数列.
的斜率是否可以按某种顺序构成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.下表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.
成绩优秀 | 成绩不够优秀 | 总计 | |
选修生涯规划课 | 15 | 10 | 25 |
不选修生涯规划课 | 6 | 19 | 25 |
总计 | 21 | 29 | 50 |
(Ⅰ)根据列联表运用独立性检验的思想方法能否有![]() 的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
(Ⅱ)如果从全校选修生涯规划课的学生中随机地抽取3名学生,求抽到成绩不够优秀的学生人数![]() 的分布列和数学期望(将频率当作概率计算).
的分布列和数学期望(将频率当作概率计算).
参考附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式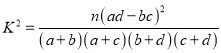 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠肺炎疫情造成医用防护服紧缺,当地政府决定为防护服生产企业A公司扩大生产提供![]() (万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到
(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到![]() (万件),其中k为工厂工人的复工率
(万件),其中k为工厂工人的复工率![]() ,A公司生产t万件防护服还需投入成本
,A公司生产t万件防护服还需投入成本![]() (万元).
(万元).
(1)将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数;
(2)对任意的![]() (万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
(万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
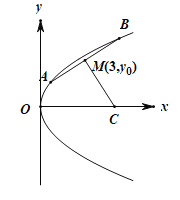
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不足120分的占![]() ,统计成绩后得到如下
,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | |||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)在上述样本中从分数不少于120分的学生中,按照分层抽样的方法,抽到线上学习时间不少于5小时和线上学习时间不足5小时的学生共5名,若在这5名学生中随机抽取2人,求至少1人每周线上学习时间不足5小时的概率.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式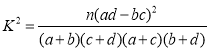 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,两焦点与短轴的一个端点的连线构成的三角形面积为
,两焦点与短轴的一个端点的连线构成的三角形面积为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)设与圆![]() 相切的直线
相切的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(
两点(![]() 为坐标原点),
为坐标原点),![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,过右焦点F的直线l与椭圆E交于A,B两点(A,B两点不在x轴上),椭圆E在A,B两点处的切线交于P,点P在定直线
,过右焦点F的直线l与椭圆E交于A,B两点(A,B两点不在x轴上),椭圆E在A,B两点处的切线交于P,点P在定直线![]() 上.
上.
(1)记点![]() ,求过点
,求过点![]() 与椭圆E相切的直线方程;
与椭圆E相切的直线方程;
(2)以![]() 为直径的圆过点F,求
为直径的圆过点F,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com