Question

【题目】已知函数， ，且曲线在处的切线方程为.

（1）求， 的值；

（2）求函数在上的最小值；

（3）证明：当时， .

Answer 1

【答案】(1) (2) （3）见解析

【解析】试题分析：（1）求出f（x）的导数，计算， ，求出a，b的值即可；

（2）求出f（x）的导数，得到导函数的单调性，得到f（x）在[0，1]递增，从而求出f（x）的最大值；

（3）只需证明x＞0时， ，因为，且曲线在处的切线方程为，故可猜测：当且时， 的图象恒在切线的上方．

试题解析：

（1）由题设得，∴，

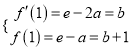解得， ．

（2）由（1）知， ，

令函数，∴，

当时， ， 递减；

当时， ， 递增；∴，即

∴当时， ，且仅当时，

故在上单调递增，

∴；

（3）由题要证：当时， ，

即证： ，

因为，且曲线在处的切线方程为，

故可猜测：当且时， 的图象恒在切线的上方．

下面证明：当时， ，

证明：设， ，

则，令， ，

当时， ， 单调递减；

当时， ， 单调递增，

又， ， ，

所以，存在，使得，

当时， ；当，

故在上单调递增，在上单调递减，在上单调递增．

又，∴，当且仅当时取等号．

故．

由（2）知， ，故，∴，当且仅当时取等号．

所以， ．

即．所以， ，

即成立，当时等号成立.

故：当时， ， 12分

方法二：要证，等价于，又，可转化为证明

令，

，

，因此当时， ， 单调递增；当时， ， 单调递减；

有最大值，即恒成立，即当时，