
分析 (Ⅰ)根据A=2C,由正弦定理化简,将$\frac{a}{c}$的比值转化为三角函数问题,利用三角函数的有界限可得取值范围.
(Ⅱ)根据b=1,c=3,A=2C.建立方程求出a和sinC,可得△ABC的面积.
解答 解:(Ⅰ)由题意:A=2C.
由正弦定理可得,$\frac{a}{c}=\frac{sinA}{sinC}=\frac{sin2C}{sinC}=2cosC$,
∵△ABC为锐角三角形,
∴$\left\{\begin{array}{l}0<A<\frac{π}{2}\\ 0<B<\frac{π}{2}\\ 0<C<\frac{π}{2}\end{array}\right.⇒\left\{\begin{array}{l}0<2C<\frac{π}{2}\\ 0<π-3C<\frac{π}{2}\\ 0<C<\frac{π}{2}\end{array}\right.⇒\frac{π}{6}<C<\frac{π}{4}$,
进而可知,$\frac{{\sqrt{2}}}{2}<cosC<\frac{{\sqrt{3}}}{2}$,
即$\frac{a}{c}$的取值范围是$(\sqrt{2},\sqrt{3})$;
(Ⅱ)由(Ⅰ)可知,$\frac{a}{c}=2cosC$,
∴a=2ccosC=6cosC,
由余弦定理可知,c2=a2+b2-2abcosC,即9=36cos2C+1-12cos2C,
∵A=2C,
∴C为锐角,
解得$cosC=\frac{{\sqrt{3}}}{3}$,
∴$sinC=\frac{{\sqrt{6}}}{3}$,$a=6cosC=2\sqrt{3}$
从而△ABC的面积为$S=\frac{1}{2}absinC=\sqrt{2}$.
(由sinB=sin3C=3sinC-4sin3C结合正弦定理求得$sinC=\frac{{\sqrt{6}}}{3}$亦可)
点评 本题考查解三角形的基础知识与基本运算,难度不大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [2,4) | C. | [2,+∞) | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
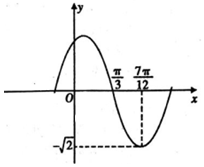 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )| A. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | B. | [-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | C. | [-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) | D. | [$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com