
���� ����������Ҷͼ��
��II������A��B���������ݵ�ƽ��ֵ���Ƚϼ��ɵó����ۣ�
������A����������������19������a��3����
B������������в�����21������bҲ��3����
�����оٷ������A���B������������и������ȡһ���Ļ����¼����������Ӧ�ĸ��ʣ�
��� 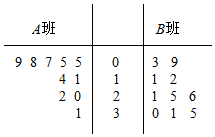 �⣺����Ҷͼ���£�ͼ�еľ���ʾʮλ���֣�Ҷ��ʾ��λ���֣���
�⣺����Ҷͼ���£�ͼ�еľ���ʾʮλ���֣�Ҷ��ʾ��λ���֣���
�Ӿ�Ҷͼ�пɿ�����
��A��������$\frac{9}{10}$�����ھ�0��1��2�ϣ�B��������$\frac{8}{10}$�����ھ�1��2��3�ϣ�
��A��Ҷ�ķֲ��ǵ���ģ�B��Ҷ�ķֲ��������ǶԳƵģ�
��A�����ݵ���λ����10��B�����ݵ���λ����23��
����A���������ݵ�ƽ��ֵΪ$\overline{x_��}=\frac{1}{10}��5+5+7+8+9+11+14+20+22+31��=13.2$Сʱ��
B���������ݵ�ƽ��ֵΪ$\overline{x_��}=\frac{1}{10}��3+9+11+12+21+25+26+30+31+35��=20.3$Сʱ��
��Ϊ$\overline{x_��}��\overline{x_��}$�������ɴ˹���B��ѧ��ƽ���ۿ�ʱ��ϳ���
����A������������в�����11������a��6�����ֱ�Ϊ5��5��7��8��9��11��B������������в�����11������b��3�����ֱ�Ϊ3��9��11��
������A���B��������и������ȡһ������Ϊ��a��b�����ֱ�Ϊ����5��3������5��9������5��11������5��3������5��9������5��11������7��3������7��9������7��11������8��3������8��9������8��11����9��3������9��9������9��11������11��3������11��9������11��11����18�֣�
����a��b���У���5��3������5��3������7��3������8��3������9��3������11��3������11��9������7�֣�
��a��b�ĸ���Ϊ$P=\frac{7}{18}$��
���� ���⿼���˾�Ҷͼ�Լ�ƽ������Ӧ�����⣬Ҳ�������оٷ���ŵ���͵ĸ������⣬�ǻ����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{4\sqrt{5}}}{5}$ | B�� | $\frac{{\sqrt{55}}}{5}$ | C�� | $\sqrt{19}$ | D�� | $\frac{{\sqrt{33}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���������ģ��ķ������Թ���ͼ��������y=$\frac{{x}^{2}}{2}$����ֱ��x=2��y=0��Χ�ɵ���
��ͼ���������ģ��ķ������Թ���ͼ��������y=$\frac{{x}^{2}}{2}$����ֱ��x=2��y=0��Χ�ɵ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1+i | B�� | 1-i | C�� | -1+i | D�� | -1-i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{3\sqrt{2}}}{4}$ | B�� | $\frac{{9\sqrt{2}}}{4}$ | C�� | $\frac{{3\sqrt{2}}}{2}$ | D�� | $\frac{{9\sqrt{2}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com