解:(Ⅰ)∵

=[f(x)+2f'(1)]

-ln(x+1)

,且A、B、C在直线l上,
∴f(x)+2f'(1)-ln(x+1)=1,(2分)
∴y=f(x)=ln(x+1)+1-2f'(1),f'(x)=

,于是f'(1)=

,
∴f(x)=ln(x+1)(4分)
(Ⅱ)令g(x)=f(x)-

,由g'(x)=

-
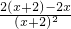
=
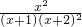
,
以及x>0,知g'(x)>0,∴g(x)在(0,+∞)上为增函数,又g(x)在x=0处右连续,
∴当x>0时,得g(x)>g(0)=0,∴f(x)>

(8分)
(Ⅲ)原不等式等价于

,
令h(x)=
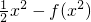
=
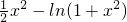
,则h'(x)=
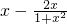
=
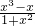
,(10分)
∵x∈(-1,0)时,h'(x)>0,x∈(0,1)时,h'(x)<0,
∴h(x)在(-1,0)为增函数,在(0,1)上为减函数,(11分)
∴当x∈[-1,1]时,h(x)
max=h(0)=0,从而依题意有0≤m
2-2m-3,
解得m≥3或m≤-1,故m的取值范围是(-∞,-1]∪[3,+∞)(12分)
分析:(Ⅰ)先利用从同一点出发终点在一条线上的三向量间的关系得到f(x)+2f'(1)-ln(x+1)=1,再求出y=f(x)的表达式,进而求出f'(1),找到f(x)=ln(x+1).
(Ⅱ)令g(x)=f(x)-

,利用导函数找出g(x)在(0,+∞)上的单调性,可得结论.
(Ⅲ)h(x)=
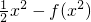
,转化为找h(x)在x∈[-1,1]上的最大值,让找出的最大值小于等于m
2-2m-3即可.
点评:本题是函数和向量的一道综合题,在解题过程中用到从同一点出发终点在一条线上的三向量间的关系,即系数和为1这一结论.而后两问都用到了利用导函数求原函数的单调性,这是一道中档难度的题.

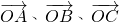 满足
满足 =[f(x)+2f′(1)]
=[f(x)+2f′(1)] -ln(x+1)
-ln(x+1) .
. ;
; x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围. =[f(x)+2f'(1)]
=[f(x)+2f'(1)] -ln(x+1)
-ln(x+1) ,且A、B、C在直线l上,
,且A、B、C在直线l上, ,于是f'(1)=
,于是f'(1)= ,
, ,由g'(x)=
,由g'(x)= -
-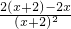 =
=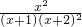 ,
, (8分)
(8分) ,
,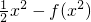 =
=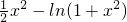 ,则h'(x)=
,则h'(x)=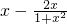 =
=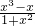 ,(10分)
,(10分) ,利用导函数找出g(x)在(0,+∞)上的单调性,可得结论.
,利用导函数找出g(x)在(0,+∞)上的单调性,可得结论.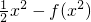 ,转化为找h(x)在x∈[-1,1]上的最大值,让找出的最大值小于等于m2-2m-3即可.
,转化为找h(x)在x∈[-1,1]上的最大值,让找出的最大值小于等于m2-2m-3即可.

 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案