
分析 直接利用函数奇偶性的概念判断①;举例说明②错误;由奇函数的性质结合周期函数的定义判断③.
解答 解:①若函数f(x)定义域为R,由g(-x)=f(-x)-f(x)=-[f(x)-f(-x)]=-g(x),可得g(x)是奇函数,故①正确;
②已知x1和x2是函数定义域内的两个值(x1<x2),若f(x1)>f(x2),则f(x)在定义域内单调递减,错误,如y=x2,-3<2,(-3)2>22,但函数y=x2在定义域内不单调;
③若f(x)是定义在R上的奇函数,则f(-x)=-f(x),又f(x+2)也是奇函数,∴f(-x+2)=-f(x+2)=f(-x-2),以-x-2替换x,得f(x+4)=f(x),则f(x)是以4为周期的周期函数,故③正确.
故答案为:①③.
点评 本题考查命题的真假判断与应用,考查了与抽象函数有关的函数的性质的应用,是中档题.


科目:高中数学 来源: 题型:选择题
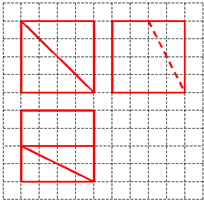 如图,网格纸上小正方形的边长为$\frac{1}{2}$,粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为$\frac{1}{2}$,粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | $\frac{20}{3}$ | B. | $\frac{25}{3}$ | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{3}{2}$i | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,0,-1} | B. | {1,-1} | C. | {-1} | D. | {0,1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com