
【题目】设![]() 为等差数列
为等差数列![]() 的前n项和,
的前n项和,![]() 是正项等比数列,且
是正项等比数列,且![]() ,
,![]() .在①
.在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,回答下列为题:
这三个条件中任选一个,回答下列为题:
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)如果![]() (m,
(m,![]() ),写出m,n的关系式
),写出m,n的关系式![]() ,并求
,并求![]() .
.
【答案】(1)见解析;(2)![]() ;
;![]()
【解析】
(1)若选①②,结合等差数列与等比数列通项公式的基本量计算,即可求得公差和公比,即可求得数列![]() 和
和![]() 的通项公式;若选③,结合等差数列前n项和公式、等差数列与等比数列通项公式,即可求得公差和公比,即可求得数列
的通项公式;若选③,结合等差数列前n项和公式、等差数列与等比数列通项公式,即可求得公差和公比,即可求得数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)根据数列![]() 和
和![]() 的通项公式,即可由
的通项公式,即可由![]() 得m,n的关系式
得m,n的关系式![]() ,利用分组求和法即可求得
,利用分组求和法即可求得![]() .
.
(1)若选①:
设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为q(
的公比为q(![]() ),
),
则![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
则![]() ,
,![]() ,
,
若选②:
设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为q(
的公比为q(![]() ),
),
则由![]() 得
得![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
若选③:
设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为q(
的公比为q(![]() ),
),
则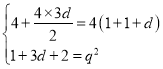 ,解得
,解得![]() 或
或![]() (舍),
(舍),
则![]() ,
,![]() .
.
(2)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
![]()
![]()
![]()
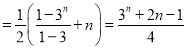 .
.


科目:高中数学 来源: 题型:
【题目】过抛物线![]() 上点
上点![]() 作三条斜率分别为
作三条斜率分别为![]() ,
,![]() ,
,![]() 的直线
的直线![]() ,
,![]() ,
,![]() ,与抛物线分别交于不同于
,与抛物线分别交于不同于![]() 的点
的点![]() .若
.若![]() ,
,![]() ,则以下结论正确的是( )
,则以下结论正确的是( )
A.直线![]() 过定点B.直线
过定点B.直线![]() 斜率一定
斜率一定
C.直线![]() 斜率一定D.直线
斜率一定D.直线![]() 斜率一定
斜率一定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
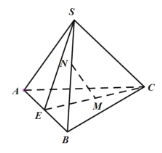
(1)证明:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置并给出证明,若不存在,说明理由;
的位置并给出证明,若不存在,说明理由;
(3)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 与
与![]() 满足的关系;
满足的关系;
(2)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(3)当![]() 时,对任意的
时,对任意的![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某市国庆节7天假期的商品房日认购量(单位:套)与日成交量(单位:套)的折线图,则下面结论中正确的是( )
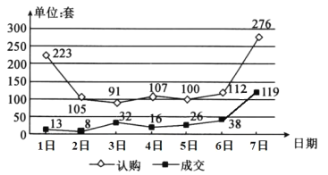
A.日成交量的中位数是16
B.日成交量超过日平均成交量的有1天
C.日认购量与日期是正相关关系
D.日认购量的方差大于日成交量的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为常数,
为常数, ![]() ,函数
,函数![]() ,
, ![]() (其中
(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)过坐标原点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求证:
,求证: ![]() ;
;
(2)令![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com