
【题目】已知![]() 为常数,
为常数, ![]() ,函数
,函数![]() ,
, ![]() (其中
(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)过坐标原点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求证:
,求证: ![]() ;
;
(2)令![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)先对函数求导, ![]() ,可得切线的斜率
,可得切线的斜率![]() ,即
,即![]() ,由
,由![]() 是方程的解,且
是方程的解,且![]() 在
在![]() 上是增函数,可证;(2)由
上是增函数,可证;(2)由![]() ,
, 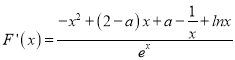 ,先研究函数
,先研究函数![]() ,则
,则![]() ,由
,由![]() 在
在![]() 上是减函数,可得
上是减函数,可得![]() ,通过研究
,通过研究![]() 的正负可判断
的正负可判断![]() 的单调性,进而可得函数
的单调性,进而可得函数![]() 的单调性,可求出参数范围.
的单调性,可求出参数范围.
试题解析:(1)![]() (
(![]() ),
),
所以切线的斜率![]() ,
,
整理得![]() ,显然,
,显然, ![]() 是这个方程的解,
是这个方程的解,
又因为![]() 在
在![]() 上是增函数,
上是增函数,
所以方程![]() 有唯一实数解,
有唯一实数解,
故![]() .
.
(2)![]() ,
, 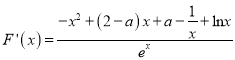 ,
,
设![]() ,则
,则![]() ,
,
易知![]() 在
在![]() 上是减函数,从而
上是减函数,从而![]() .
.
①当![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 上是增函数,
上是增函数,
∵![]() ,∴
,∴![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() 在区间
在区间![]() 上是减函数,所以
上是减函数,所以![]() 满足题意.
满足题意.
②当![]() ,即
,即![]() 时,设函数
时,设函数![]() 的唯一零点为
的唯一零点为![]() ,
,
则![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
又∵![]() ,∴
,∴![]() ,
,
又∵![]() ,
,
∴![]() 在
在![]() 内有唯一一个零点
内有唯一一个零点![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
从而![]() 在
在![]() 递减,在
递减,在![]() 递增,与在区间
递增,与在区间![]() 上是单调函数矛盾.
上是单调函数矛盾.
∴![]() 不合题意.综上①②得,
不合题意.综上①②得, ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() 为等差数列
为等差数列![]() 的前n项和,
的前n项和,![]() 是正项等比数列,且
是正项等比数列,且![]() ,
,![]() .在①
.在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,回答下列为题:
这三个条件中任选一个,回答下列为题:
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)如果![]() (m,
(m,![]() ),写出m,n的关系式
),写出m,n的关系式![]() ,并求
,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,点
,点![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程.
的轨迹方程.
(2)设点![]() ,
,![]() 是
是![]() 的轨迹上异于顶点的任意两点,以
的轨迹上异于顶点的任意两点,以![]() 为直径的圆过点
为直径的圆过点![]() .求证直线
.求证直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,右表是对 100 辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.
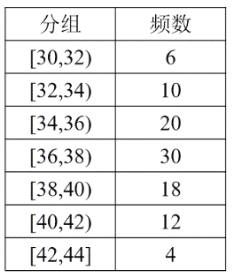
(Ⅰ)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(Ⅱ)用分层抽样的方法从行车里程在区间[38,40)与[40,42)的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在[40,42)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)当m=1时,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ,
,![]() ).
).
(1)当![]() 时,
时,![]() 在
在![]() 上是单调递增函数,求
上是单调递增函数,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,讨论函数
时,讨论函数![]() 的单调区间;
的单调区间;
(3)对于任意给定的正实数![]() ,证明:存在实数
,证明:存在实数![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】影响消费水平的原因很多,其中重要的一项是工资收入.研究这两个变量的关系的一个方法是通过随机抽样的方法,在一定范围内收集被调查者的工资收入和他们的消费状况.下面的数据是某机构收集的某一年内上海、江苏、浙江、安徽、福建五个地区的职工平均工资与城镇居民消费水平(单位:万元).
地区 | 上海 | 江苏 | 浙江 | 安徽 | 福建 |
职工平均工资 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城镇居民消费水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江苏、浙江、安徽三个地区的职工平均工资和他们的消费水平,求出线性回归方程![]() ,其中
,其中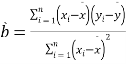
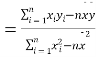 ,
,![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1万,则认为得到的线性回归方程是可靠的,试问所得的线性回归方程是否可靠?(![]() 的结果保留两位小数)
的结果保留两位小数)
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AA1![]() AB
AB![]() AC
AC![]() 2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
(1)若P是线段A1B的中点,求直线MP与直线AC所成角的大小;
(2)若![]() 是
是![]() 的中点,直线
的中点,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段BP的长度.
,求线段BP的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com