【题目】在△ABC中，角A,B,C的对边分别是a，b，c，已知
(1）求
的值；
(2）若
，求边c的值.
【答案】（1）
；（2）
或
【解析】
（1）利用正弦定理化简已知的等式，再利用两角和与差的正弦函数公式及诱导公式化简，并根据sinA的值不为0，即可求出cosA的值；
（2）由第一问求出的cosA的值及A的范围，利用特殊角的三角函数值求出A的度数，进而得出B+C的度数，用B表示出C，代入已知的等式中，利用两角和与差的余弦函数公式化简，整理后再利用两角和与差的正弦函数公式化简，求出sin（B+
）的值，由A的度数求出B+的范围，利用特殊角的三角函数值得出B的度数，根据锐角三角函数定义即可求出c的值．
（1）由
及正弦定理得
即
又
所以有
即
而
，所以
(2）由
及0＜A＜
，得A＝
因此
由
得
即
，即得
由
知
于是
或
所以
，或
若
则
在直角△ABC中，
，解得
若
在直角△ABC中，
解得
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知数列{an}满足a1=1，an+1= 
（n∈N*），若bn+1=（n﹣2λ）（ 
+1）（n∈N*），b1=﹣λ，且数列{bn}是单调递增数列，則实数λ的取值范围是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
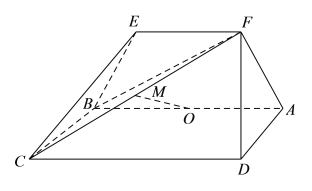
【题目】如图，等腰梯形
中，
，
，
，
，
为
的中点，矩形
所在的平面和平面互相垂直．
（
）求证：
平面
．
（
）设
的中点为
，求证：
平面
．
（
）求三棱锥
的体积．（只写出结果，不要求计算过程）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知在△ABC中，角A，B，C所对的边分别为a，b，c，且2sin Acos B=2sin C﹣sin B． ①求角A；
②若a=4 
，b+c=8，求△ABC 的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图甲所示，放在水平地面上的物体，受到方向不变的水平推力F的作用，F的大小与时间t的关系和物体运动速度v与时间t的关系如图乙所示．下列判断正确的是：
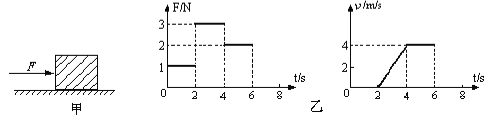
A.t＝3s时，物体受到力的合力为零
B.t＝6s时，将F撤掉，物体立刻静止
C.2s～4s内物体所受摩擦力逐渐增大
D.t＝1s时，物体所受摩擦力是1N
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】抛掷两枚骰子，求：
（1）点数之和为4的倍数的概率；
（2）点数之和大于5而小于10的概率；
（3）同时抛两枚骰子，求至少有一个5点或者6点的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】用数学归纳法证明“
能被3整除”的第二步中，
时，为了使用假设，应将5k＋1－2k＋1变形为( )．
A. (5k－2k)＋4×5k－2k B. 5(5k－2k)＋3×2k
C. (5－2)(5k－2k) D. 2(5k－2k)－3×5k
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知在平面直角坐标系中，椭圆C的参数方程为 
（θ为参数）．
（1）以原点为极点，x轴的正半轴为极轴建立极坐标系，求椭圆C的极坐标方程；
（2）设M（x，y）为椭圆C上任意一点，求x+2y的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
