
【题目】用数学归纳法证明“![]() 能被3整除”的第二步中,
能被3整除”的第二步中,![]() 时,为了使用假设,应将5k+1-2k+1变形为( ).
时,为了使用假设,应将5k+1-2k+1变形为( ).
A. (5k-2k)+4×5k-2k B. 5(5k-2k)+3×2k
C. (5-2)(5k-2k) D. 2(5k-2k)-3×5k
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinxcos(x+ ![]() )+
)+ ![]() .
.
(1)求函数f(x)的单调递减区间;
(2)求函数f(x)在区间[0, ![]() ]上的最大值及最小值.
]上的最大值及最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+1的图象向左平移
cos2x+1的图象向左平移 ![]() 个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
A.函数y=g(x)的最小正周期为π
B.函数y=g(x)的图象的一条对称轴为直线x= ![]()
C.![]() g(x)dx=
g(x)dx= ![]()
D.函数y=g(x)在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A,B,C所对的边分别为a,b,c,且2sin Acos B=2sin C﹣sin B. ①求角A;
②若a=4 ![]() ,b+c=8,求△ABC 的面积.
,b+c=8,求△ABC 的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某闯关游戏规则是:先后掷两枚骰子,将此试验重复n轮,第n轮的点数分别记为xn , yn , 如果点数满足xn< ![]() ,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
(Ⅰ)求第一轮闯关成功的概率;
(Ⅱ)如果第i轮闯关成功所获的奖金数f(i)=10000× ![]() (单位:元),求某人闯关获得奖金不超过1250元的概率;
(单位:元),求某人闯关获得奖金不超过1250元的概率;
(Ⅲ)如果游戏只进行到第四轮,第四轮后不论游戏成功与否,都终止游戏,记进行的轮数为随机变量X,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
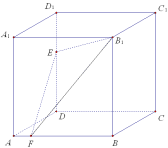
【题目】如图,正方体![]() 中,
中,![]() ,
,![]() 分别为 棱
分别为 棱![]() ,
,![]() 上的点. 已知下列判断:
上的点. 已知下列判断:
①![]() 平面
平面![]() ;②
;②![]() 在侧面
在侧面![]() 上 的正投影是面积为定值的三角形;③在平面
上 的正投影是面积为定值的三角形;③在平面![]() 内总存在与平面
内总存在与平面![]() 平行的直线;④平 面
平行的直线;④平 面![]() 与平面
与平面![]() 所成的二面角(锐角)的大小与点
所成的二面角(锐角)的大小与点![]() 的位置有关,与点
的位置有关,与点![]() 的位置无关.
的位置无关.
其中正确判断的个数有
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com