
| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬q | B. | p∧q | C. | ¬p∧q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为
如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.
某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
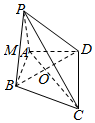 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com