
 某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.
某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.分析 (Ⅰ)由频率分布直方图得:a:b=3:4,(0.01+a+b+0.06+b+0.02)×5,由此能求出a,b.
(Ⅱ)(ⅰ)由(Ⅰ)可知a=0.03,b=0.04,由此利用频率分布直方图能求出按现有的物价水平,抚养一个孩子平均要花多少钱.
(ii)数据在区间[30,35)上的人数为15人,[40,45)上的人数为30人,按分层抽样的方法在数据在区间[30,35)和[40,45)上的接受调查的市民中选取6人参加电视台举办的访谈,则在[30,35)上选取2人,在[40,45)上选取4人,再从这6人中随机选取2人,能求出数据在[30,35)的市民中至少有一人被选中的概率.
解答 解:(Ⅰ)∵样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4,
∴由频率分布直方图得:a:b=3:4①
由频率分布直方图得:(0.01+a+b+0.06+b+0.02)×5②…(1分)
由①得$a=\frac{3}{4}b$代入②得:$(0.09+\frac{11b}{4})×5=1$…(2分)
解得:b=0.04…(3分)
∴a=0.03…(4分)
(Ⅱ)(ⅰ)由(Ⅰ)可知a=0.03,b=0.04
根据直方图可得:
按现有的物价水平,抚养一个孩子平均要花:
(27.5×0.01+32.5×0.03+37.5×0.04+42.5×0.06+47.5×0.04+52.5×0.02)×5=41.25(万元).
(ii)由(Ⅰ)得数据在区间[30,35)上的人数为0.03×5×100=15人,[40,45)上的人数为0.06×5×100=30人,
按分层抽样的方法在数据在区间[30,35)和[40,45)上的接受调查的市民中选取6人参加电视台举办的访谈,
则在[30,35)上选取$\frac{15}{15+30}$×6=2人,在[40,45)上选取$\frac{30}{15+30}×6$=4人,
再从这6人中随机选取2人,则数据在[30,35)的市民中至少有一人被选中的概率:
P=1-$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是中档题,解题时要认真审题,注意对立事件、分层抽样的性质的合理运用.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
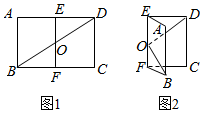 如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中:
如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\frac{{2\sqrt{3}}}{3}})$ | B. | $({\frac{{2\sqrt{3}}}{3},2})$ | C. | $(1,\sqrt{3})$ | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 语言表达能力 人数 逻辑思维能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | 1 |
| 良好 | 4 | m | 1 |
| 优秀 | 1 | 3 | n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{\sqrt{6}}{4}$x | B. | y=±$\frac{2\sqrt{6}}{3}$x | C. | y=±2$\sqrt{2}$x | D. | y=±$\frac{2\sqrt{3}}{3}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com