
| 语言表达能力 人数 逻辑思维能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | 1 |
| 良好 | 4 | m | 1 |
| 优秀 | 1 | 3 | n |
分析 (1)根据古典概型的概率列方程解出n,再根据人数之和为20得出m;
(2)使用组合数公式计算基本事件,利用古典概型的概率计算公式得出概率.
解答 解;(1)∵语言表达能力优秀或逻辑思维能力优秀的学生共有1+3+n+1+1=6+n,
抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为$\frac{2}{5}$.
∴$\frac{6+n}{20}=\frac{2}{5}$,解得n=2.
∴m=4.
(2)语言表达能力良好的学生共有2+4+3=9人.其中思维能力优秀的有3人,
则从9人中抽取2人共有${C}_{9}^{2}$=36个基本事件,而至少有一名思维能力优秀的基本事件个数为${C}_{3}^{2}$+${C}_{3}^{1}$•${C}_{6}^{1}$=21.
∴至少有一名逻辑思维能力优秀的学生的概率P=$\frac{21}{36}$=$\frac{7}{12}$.
点评 本题考查了古典概型的概率计算,属于基础题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
 某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.
某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
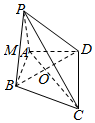 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${({\frac{1}{3}})^{\frac{1}{2}}}$ | B. | ${0.6^{\frac{1}{2}}}$ | C. | 0.6-2 | D. | ${0.6^{-\frac{3}{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$
如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com