
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,满足(2b﹣c)cosA=acosC.
(1)求角A;
(2)若 ![]() ,b+c=5,求△ABC的面积.
,b+c=5,求△ABC的面积.
【答案】
(1)解:在三角形ABC中,∵(2b﹣c)cosA=acosC,
由正弦定理得:(2sinB﹣sinC)cosA=sinAcosC,
化为:2sinBcosA=sinCcosA+sinAcosC=sin(A+C)=sinB,
sinB≠0,解得cosA= ![]() .A∈(0,π).
.A∈(0,π).
∴A= ![]() .
.
(2)解:由余弦定理得a2=b2+c2﹣2bccosA,
∵a= ![]() ,b+c=5,
,b+c=5,
∴13=(b+c)2﹣3cb=52﹣3bc,
化为bc=4,
所以三角形ABC的面积S= ![]() bcsinA=
bcsinA= ![]() ×4×
×4× ![]() =
= ![]() .
.
【解析】(1)由正弦定理进行边角互化,可得到(2sinB﹣sinC)cosA=sinAcosC,进行化简整理结合两角和的正弦公式可得2sinBcosA=sin(A+C)=sinB,不难得出cosA的值,进而得到A的角度,(2)根据余弦定理可得出bc=4,结合(1)中A的角度可得三角形的面积.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=1,前n项和为Sn , 且满足(n+1)an=2Sn(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=ancos(πan),求数列{bn)的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且an是2与Sn的等差中项.
(1)求数列{an}的通项公式;
(2)若 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对应的边分别为a,b,c,若c(acosB﹣ ![]() b)=a2﹣b2 .
b)=a2﹣b2 .
(1)求角A;
(2)若a= ![]() ,求c﹣b的取值范围.
,求c﹣b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点p(x,y)是直线kx+y+4=0(k>0)上一动点,PA、PB是圆C:x2+y2﹣2y=0的两条切线,A、B是切点,若四边形PACB的最小面积是2,则k的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记定义在R上的函数y=f(x)的导函数为f′(x).如果存在x0∈[a,b],使得f(b)﹣f(a)=f′(x0)(b﹣a)成立,则称x0为函数f(x)在区间[a,b]上的“中值点”.那么函数f(x)=x3﹣3x在区间[﹣2,2]上的“中值点”为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,点D是BC的中点.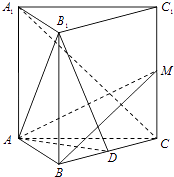
(1)求证:A1C∥平面AB1D;
(2)设M为棱CC1的点,且满足BM⊥B1D,求证:平面AB1D⊥平面ABM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=(logmx)2+2logmx﹣3(m>0,且m≠1).
(Ⅰ)当m=2时,解不等式f(x)<0;
(Ⅱ)f(x)<0在[2,4]恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com