
【题目】已知函数 ![]() ,对a∈R,b∈(0,+∞),使得f(a)=g(b),则b﹣a的最小值为( )
,对a∈R,b∈(0,+∞),使得f(a)=g(b),则b﹣a的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:∵f(x)=e2x , g(x)=lnx+ ![]() , ∴f﹣1(x)=
, ∴f﹣1(x)= ![]() lnx,g﹣1(x)=
lnx,g﹣1(x)= ![]() ,
,
令h(x)=g﹣1(x)﹣f﹣1(x)= ![]() ﹣
﹣ ![]() lnx,
lnx,
则b﹣a的最小值,即为h(x)的最小值,
∵h′(x)=)= ![]() ﹣
﹣ ![]() ,
,
令h′(x)=0,解得x= ![]() ,
,
∵当x∈(0, ![]() )时,h′(x)<0,当x∈(
)时,h′(x)<0,当x∈( ![]() ,+∞)时,h′(x)>0,
,+∞)时,h′(x)>0,
故当x= ![]() 时,h(x)取最小值1﹣
时,h(x)取最小值1﹣ ![]() =1+
=1+ ![]() ,
,
故选:A.
【考点精析】关于本题考查的函数的值域,需要了解求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin(2x+ ![]() )图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移
)图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移 ![]() 个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
A.(﹣ ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.(﹣ ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )
①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行.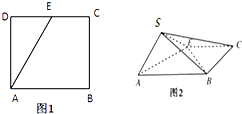
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,满足(2b﹣c)cosA=acosC.
(1)求角A;
(2)若 ![]() ,b+c=5,求△ABC的面积.
,b+c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 且Sn=n(n+1),n∈N* .
(1)求数列{an}的通项公式;
(2)若数列{bn}满足: ![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )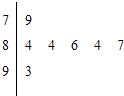
A.84,4.84
B.84,1.6
C.85,1.6
D.85,4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.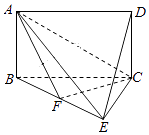
(1)求证:平面AEC⊥平面ABE;
(2)点F在BE上,若DE∥平面ACF,DC=CE= ![]() BC=3,求三棱锥A﹣BCF的体积.
BC=3,求三棱锥A﹣BCF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com