练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．用秦九韶算法计算多项式f（x）=12+35x+9x3+5x5+3x6，在当x=-1时的值，有如下的说法：①要用到6次乘法和6次加法；②要用到6次加法和8次乘法；③v0=-23； ④v3=11，其中正确的是（　　）
    A．①③B．①④C．②④D．①③④

    分析 根据秦九韶算法求多项式的规则变化其形式，把f（x）=12+35x+9x3+5x5+3x6等到价转化为f（x）=（（（（（3x+5）x+0）x+9）x+0）x+35）x+12，就能求出结果．

    解答 解：∵f（x）=12+35x+9x3+5x5+3x6=（（（（（3x+5）x+0）x+9）x+0）x+35）x+12
    ∴需做加法与乘法的次数都是6次，
    ∴v0=3，
    v1=v0x+a5=3×（-1）+5=2，
    v2=v1x+a4=2×（-1）+0=-2，
    v3=v2x+a3=-2×（-1）+9=11，
    ∴V3的值为11；
    其中正确的是①④
    故选：B．

    点评 本题考查算法的多样性，正确理解秦九韶算法求多项式的原理是解题的关键，本题是一个比较简单的题目，运算量也不大，只要细心就能够做对，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．若样本1+x1，1+x2，1+x3，…，1+xn的平均数是10，方差为2，则对于样本2+x1，2+x2，…，2+xn，下列结论正确的是（　　）
    A．平均数为10，方差为2B．平均数为11，方差为3
    C．平均数为11，方差为2D．平均数为12，方差为4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．下列命题中，正确的是（　　）
    A．|$\overrightarrow{a}$|=|$\overrightarrow{b}$|⇒$\overrightarrow{a}$=$\overrightarrow{b}$B．|$\overrightarrow{a}$|＞|$\overrightarrow{b}$|⇒$\overrightarrow{a}$＞$\overrightarrow{b}$C．|$\overrightarrow{a}$|=|$\overrightarrow{b}$|⇒$\overrightarrow{a}$∥$\overrightarrow{b}$D．|$\overrightarrow{a}$|=0⇒$\overrightarrow{a}$=$\overrightarrow{0}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．cos$\frac{5π}{6}$=-$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．直线xcosα+$\sqrt{3}$y+2=0的斜率的范围是[$-\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$]，倾斜角的范围是[0，$\frac{π}{6}$]∪[$\frac{5π}{6}$，π）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知函数f（x）=-x3-x，若实数a，b满足f（a-1）+f（b）=0，则a+b等于1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

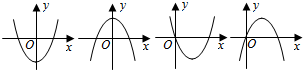
    4．下面四个图象中，有一个是函数f（x）=$\frac{1}{3}$x3+ax2+（a2-1）x+1（a∈R）的导函数y=f'（x）的图象，则f（-1）等于（　　）
    A．$\frac{1}{3}$B．-$\frac{1}{3}$C．$\frac{5}{3}$D．-$\frac{1}{3}$或$\frac{5}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知A={x|m+1≤x≤3m-1}，B={x|1≤x≤10}，且A⊆B，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知|a|=3，|b|=2，|c|=1，且a＜b＜c，求a+b+c的值．

    查看答案和解析>>

    同步练习册答案