考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)取AB中点为O,连接OD,OB1,证明AB⊥平面B1OD,可得AB⊥OD,又OD⊥BB1,因为AB∩BB1=B,即可证明平面ABB1A1⊥平面ABC;
(Ⅱ)证明B1O即点B1到平面BCD的距离,即可求三棱锥C-BB1D的体积.
解答:

(Ⅰ)证明:取AB中点为O,连接OD,OB
1.
因为B
1B=B
1A,所以OB
1⊥AB.
又AB⊥B
1D,OB
1∩B
1D=B
1,
所以AB⊥平面B
1OD,
因为OD?平面B
1OD,所以AB⊥OD.…(3分)
由已知,BC⊥BB
1,又OD∥BC,
所以OD⊥BB
1,因为AB∩BB
1=B,
所以OD⊥平面ABB
1A
1.
又OD?平面ABC,所以平面ABC⊥平面ABB
1A
1. …(6分)
(Ⅱ)解:三棱锥C-BB
1D的体积=三棱锥B
1-BCD的体积
由(Ⅰ)知,平面ABC⊥平面ABB
1A
1,平面ABC∩平面ABB
1A
1=AB,OB
1⊥AB,OB
1?平面ABB
1A
1所以OB
1⊥平面ABC,即OB
1⊥平面BCD,B
1O即点B
1到平面BCD的距离,
B1O=…(9分)
S△BCD=S△ABC=1…(11分)
所以
VC-BB1D=VB1-BCD=×1×=…(12分)
点评:本题考查平面与平面垂直的证明,考查三棱锥的体积,解题时要认真审题,注意空间思维能力的合理运用.

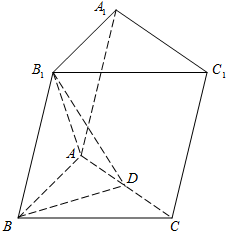 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D. (Ⅰ)证明:取AB中点为O,连接OD,OB1.
(Ⅰ)证明:取AB中点为O,连接OD,OB1.

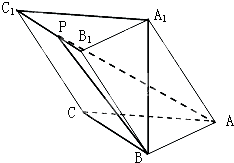 在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2
在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2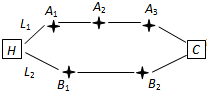 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为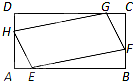 如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为
如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为