
已知函数f(x)=a-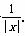 .
.
(1)求证:函数y=f(x)在(0,+∞)上是增函数;
(2)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
北京动物园在国庆节期间异常火爆,游客非常多,成人票20元一张,学生票10元一张,儿童票5元一张,假设有m个成人,n个学生,f个儿童,请编写一个程序完成售票的计费工作,并输出最后收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图1是某公共汽车线路收支差额y元与乘客量x的图象.

(1)试说明图1上点A、点B以及射线AB上的点的实际意义;
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图2、3所示.你能根据图象,说明这两种建议的意义吗?
(3)此问题中直线斜率的实际意义是什么?
(4)图1、图2、图3中的票价分别是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)的图象向左平移1个单位后关于y轴对称,当x2>x1>1时,[f(x2)-f(x1)]·(x2-x1)<0恒成立,设a=f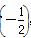 ,b=f(2),c=f(3),则a,b,c的大小关系为( )
,b=f(2),c=f(3),则a,b,c的大小关系为( )
A.c>a>b B.c>b>a C.a>c>b D.b>a>c
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二次函数f(x)=ax2+bx+c为偶函数,且f(-1)=-1.
(1)求函数f(x)的解析式;
(2)若函数g(x)=f(x)+(2-k)x在区间[-2,2]上单调递减,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com