
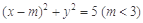 与椭圆E:
与椭圆E: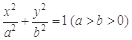 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.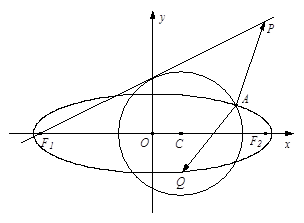
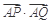 的取值范围.
的取值范围. .(Ⅱ) [-12,0].
.(Ⅱ) [-12,0].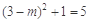 .
.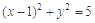 .设直线P
.设直线P 的斜率为k,
的斜率为k,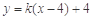 ,即
,即 .
. 与圆C相切,∴
与圆C相切,∴ .
.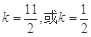 . 4分
. 4分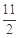 时,直线PF1与x轴的交点横坐标为
时,直线PF1与x轴的交点横坐标为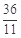 ,不合题意,舍去.
,不合题意,舍去.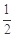 时,直线PF1与x轴的交点横坐标为-4,
时,直线PF1与x轴的交点横坐标为-4, (-4,0),
(-4,0),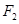 (4,0).
(4,0).  +A
+A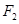 =
= ,
,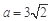 ,a2=18,b2=2.
,a2=18,b2=2. . 7分
. 7分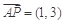 ,设Q(x,y),
,设Q(x,y),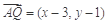 ,
,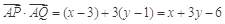 . 9分
. 9分 ,即
,即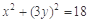 ,
,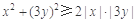 ,∴-18≤6xy≤18.
,∴-18≤6xy≤18. 的取值范围是[0,36].
的取值范围是[0,36]. 的取值范围是[-6,6].
的取值范围是[-6,6].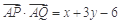 的取值范围是[-12,0]. 13分
的取值范围是[-12,0]. 13分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
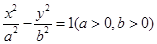 的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为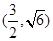 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
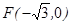 ,且过
,且过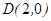 ,设点
,设点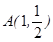 .
.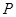 是椭圆上的动点,求线段
是椭圆上的动点,求线段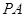 中点
中点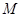 的轨迹方程。
的轨迹方程。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
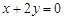 ,并经过点
,并经过点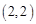 ,求此双曲线的标准方程.
,求此双曲线的标准方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com