
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() 在底面
在底面![]() 上的投影为
上的投影为![]() 的中点
的中点![]() ,
,![]() .有下列结论:
.有下列结论:
①三棱锥![]() 的三条侧棱长均相等;
的三条侧棱长均相等;
②![]() 的取值范围是
的取值范围是![]() ;
;
③若三棱锥的四个顶点都在球![]() 的表面上,则球
的表面上,则球![]() 的体积为
的体积为![]() ;
;
④若![]() ,
,![]() 是线段
是线段![]() 上一动点,则
上一动点,则![]() 的最小值为
的最小值为![]() .
.
其中所有正确结论的编号是( )
A.①②B.②③C.①②④D.①③④
科目:高中数学 来源: 题型:
【题目】在多面体![]() 中,正方形
中,正方形![]() 和矩形
和矩形![]() 互相垂直,
互相垂直,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,![]() .
.
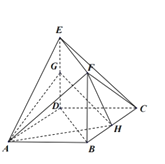
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)在![]() 边所在的直线上存在一点
边所在的直线上存在一点![]() ,使得
,使得![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合S,T,S![]() N*,T
N*,T![]() N*,S,T中至少有两个元素,且S,T满足:
N*,S,T中至少有两个元素,且S,T满足:
①对于任意x,y![]() S,若x≠y,都有xy
S,若x≠y,都有xy![]() T
T
②对于任意x,y![]() T,若x<y,则
T,若x<y,则![]()
![]() S;
S;
下列命题正确的是( )
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了![]() 天空气中的
天空气中的![]() 和
和![]() 浓度(单位:
浓度(单位:![]() ),得下表:
),得下表:
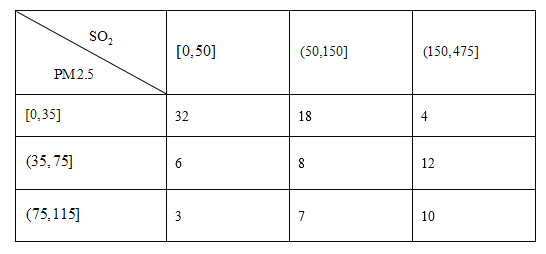
(1)估计事件“该市一天空气中![]() 浓度不超过
浓度不超过![]() ,且
,且![]() 浓度不超过
浓度不超过![]() ”的概率;
”的概率;
(2)根据所给数据,完成下面的![]() 列联表:
列联表:
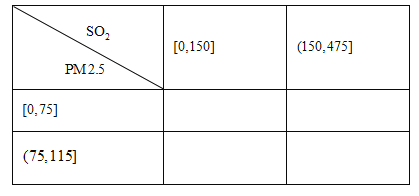
(3)根据(2)中的列联表,判断是否有![]() 的把握认为该市一天空气中
的把握认为该市一天空气中![]() 浓度与
浓度与![]() 浓度有关?
浓度有关?
附: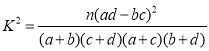 ,
,
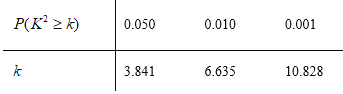
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]()
![]() ,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在△![]() 中,内角A,B,C所对的边分别为
中,内角A,B,C所对的边分别为![]() .且满足_________.
.且满足_________.
(1)求![]() ;
;
(2)已知![]() ,△
,△![]() 的外接圆半径为
的外接圆半径为![]() ,求△
,求△![]() 的边AB上的高
的边AB上的高![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
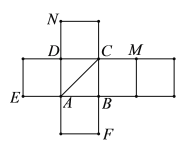
【题目】一个正方体的平面展开图如图所示,在这个正方体中,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() (不包含端点)上的动点,则下列说法正确的是( )
(不包含端点)上的动点,则下列说法正确的是( )
A.在点![]() 的运动过程中,存在
的运动过程中,存在![]()
B.在点![]() 的运动过程中,存在
的运动过程中,存在![]()
C.三棱锥![]() 的体积为定值
的体积为定值
D.三棱锥![]() 的体积不为定值
的体积不为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为加强对销售员的考核与管理,从销售部门随机抽取了2019年度某一销售小组的月均销售额,该小组各组员2019年度的月均销售额(单位:万元)分别为:3.35,3.35,3.38,3.41,3.43,3.44,3.46,3.48,3.51,3.54,3.56,3.56,3.57,3.59,3.60,3.64,3.64,3.67,3.70,3.70.
(Ⅰ)根据公司人力资源部门的要求,若月均销售额超过3.52万元的组员不低于全组人数的![]() ,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
(Ⅱ)在该销售小组中,已知月均销售额最高的5名销售员中有1名的月均销售额造假.为找出月均销售额造假的组员,现决定请专业机构对这5名销售员的月均销售额逐一进行审核,直到能确定出造假组员为止.设审核次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线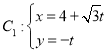 (t为参数),曲线
(t为参数),曲线![]() ,(
,(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系.
为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 分别交
分别交![]() ,
,![]() 于A,B两点,求
于A,B两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com