Question

19．斜率为k（k＞0）的直线经过抛物线y²=2px（p＞0）的焦点，与抛物线交于A、B两点，与抛物线的准线交于C点，当B为AC中点时，k的值为（　　）

• A． $\frac{\sqrt{2}}{4}$
• B． $\sqrt{2}$
• C． 2$\sqrt{2}$
• D． 3$\sqrt{2}$

Answer 1

分析 如图，设A，B两点的抛物线的准线上的射影分别为E，M，过B作AE的垂线BN，在三角形ABN中，∠BAN等于直线AB的倾斜角，其正切值即为k值，利用在直角三角形ABN中，tan∠BAN=$\frac{BN}{AN}$，从而得出直线AB的斜率．

解答 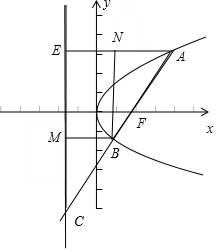解：如图，设A，B两点的抛物线的准线上的射影分别为E，M，
过B作AE的垂线BN，
在三角形ABN中，∠BAN等于直线AB的倾斜角，其正切值即为k值，
设|BF|=n，B为AC中点，可得2|BF|=|AE|，即|AF|=2|BF|，∴|AF|=2n，
根据抛物线的定义得：|AE|=2n，|BF|=n，
∴|AN|=n，
在直角三角形ABC中，tan∠BAN=$\frac{BN}{AN}$=$\frac{\sqrt{9{n}^{2}-{n}^{2}}}{n}$=2$\sqrt{2}$；
故选：C．

点评 本题主要考察了直线与抛物线的位置关系，抛物线的简单性质，特别是焦点弦问题，解题时要善于运用抛物线的定义解决问题．