
分析 设直线l:x+y=1上任意一点M(x,y)在矩阵A的变换作用下,变换为点M′(x′,y′),根据矩阵A列出关系式,得到x与x′,y与y′的关系式,再由M′(x′,y′)在直线l'上,求出m与n的值,即可确定出矩阵A.
解答 解:设直线l:x+y=1上任意一点M(x,y)在矩阵A的变换作用下,变换为点M′(x′,y′),
由[$\underset{\stackrel{x′}{\;}}{y′}$]=[$\underset{\stackrel{m}{\;}}{0}$ $\underset{\stackrel{n}{\;}}{1}$][$\underset{\stackrel{x}{\;}}{y}$]=[$\underset{\stackrel{mx+ny}{\;}}{y}$],得$\left\{\begin{array}{l}{x′=mx+ny}\\{y′=y}\end{array}\right.$,
又点M′(x′,y′)在l′:x-y=1上,
∴x′-y′=1,即(mx+ny)-y=1,
依题意$\left\{\begin{array}{l}{m=1}\\{n-1=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=1}\\{n=2}\end{array}\right.$,
则矩阵A=[$\underset{\stackrel{1}{\;}}{0}$ $\underset{\stackrel{2}{\;}}{1}$].
点评 此题考查了几种特殊的矩形变换,找出M在矩阵A的变换作用下点M′两点的坐标关系是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{30}$ | B. | $\frac{13}{30}$ | C. | $\frac{11}{25}$ | D. | $\frac{13}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
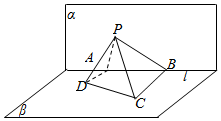 如图,已知平面α∩平面β=l,α⊥β,A,B是直线l上的两点,C,D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8,P是平面α内的一动点,使得直线CP,DP与平面α所成角相等,则三角形PAB面积的最大值为12.
如图,已知平面α∩平面β=l,α⊥β,A,B是直线l上的两点,C,D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8,P是平面α内的一动点,使得直线CP,DP与平面α所成角相等,则三角形PAB面积的最大值为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com