
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 令f(x)<0可解x的范围确定①正确;对函数f(x)进行求导,然后令f'(x)=0求出x,根据f'(x)的正负判断原函数的单调性,求出函数的极值进而可确定②正确;根据函数的单调性可判断函数的取值范围判断③正确,解方程判断④不正确,从而得到答案.
解答 解:由f(x)<0⇒(x2-2x)ex<0⇒x2-2x<0⇒0<x<2,
故①正确;
f′(x)=ex(x2-2),由f′(x)=0得x=±$\sqrt{2}$,
由f′(x)>0得x>$\sqrt{2}$或x<-$\sqrt{2}$,由f′(x)<0得-$\sqrt{2}$<x<$\sqrt{2}$,
∴f(x)的单调增区间为(-∞,-$\sqrt{2}$),($\sqrt{2}$,+∞).单调减区间为(-$\sqrt{2}$,$\sqrt{2}$).
∴f(x)的极小值为f($\sqrt{2}$),极大值为f(-$\sqrt{2}$),故②正确;
而f($\sqrt{2}$)=(2-2$\sqrt{2}$)${e}^{\sqrt{2}}$<0,f(-$\sqrt{2}$)=(2+2$\sqrt{2}$)${e}^{-\sqrt{2}}$>0,
x>2时,f(x)>0恒成立,x<0时,f(x)>0恒成立,x→-∞时,f(x)→0,
∴f(x)没有最大值,有最小值,最小值是f($\sqrt{2}$),∴③正确,
令f(x)=0,解得:x=0或x=2,f(x)有2个零点,④不正确.
故选:C.
点评 本题主要考查函数的极值与其导函数关系,即函数取到极值时导函数一定等于0,但导函数等于0时还要判断原函数的单调性才能确定原函数的极值点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
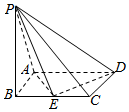 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,E为BC的中点,AB=1,AD=2,PA=2.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,E为BC的中点,AB=1,AD=2,PA=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
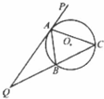 如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,使得QC2-QA2=BA•QC.
如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,使得QC2-QA2=BA•QC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | $1+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
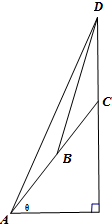 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD.为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进25m到达B处,又测得∠DBC=45°.根据以上数据计算可得cosθ=$\frac{\sqrt{3}-1}{2}$.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD.为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进25m到达B处,又测得∠DBC=45°.根据以上数据计算可得cosθ=$\frac{\sqrt{3}-1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com