
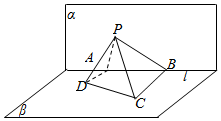
 如图,已知平面α∩平面β=l,α⊥β,A,B是直线l上的两点,C,D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8,P是平面α内的一动点,使得直线CP,DP与平面α所成角相等,则三角形PAB面积的最大值为12.
如图,已知平面α∩平面β=l,α⊥β,A,B是直线l上的两点,C,D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8,P是平面α内的一动点,使得直线CP,DP与平面α所成角相等,则三角形PAB面积的最大值为12. 分析 由面面垂直的性质可得AD⊥PA,BC⊥PB,由∠APD=∠BPC可知PB=2PA,作PM⊥AB,垂足为M,结合三角形的面积公式转化为一元二次函数进行求解即可.
解答  解:由题意平面α⊥平面β,A、B是平面α与平面β的交线上的两个定点,DA?β,CB?β,且DA⊥α,CB⊥α,
解:由题意平面α⊥平面β,A、B是平面α与平面β的交线上的两个定点,DA?β,CB?β,且DA⊥α,CB⊥α,
∴△PAD与△PBC是直角三角形,又∠APD=∠BPC,
∴△PAD∽△PBC,又AD=4,BC=8,
∴PB=2PA
作PM⊥AB,垂足为M,令AM=t∈R,
在两个Rt△PAM与Rt△PBM中,PM是公共边及PB=2PA
∴PA2-t2=4PA2-(6-t)2
解得PA2=12-4t
∴PM=$\sqrt{12-4t-{t}^{2}}$
∴S=$\frac{1}{2}$×AB×PM=$\frac{1}{2}$×6×$\sqrt{12-4t-{t}^{2}}$=3$\sqrt{12-4t-{t}^{2}}$
=3$\sqrt{16-{(t+2)}^{2}}$≤12.
即三角形面积的最大值为12.
故答案为:12
点评 本题考查与二面角有关的立体几何综合题,根据线面角的定义结合三角形的面积公式,设出变量,转化为函数问题是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 4 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(?q) | C. | (?p)∧q | D. | (?p)∧(?q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 135° | C. | 150° | D. | 105° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com