
分析 (1)设焦点F(0,m),圆C:x2+(y-4)2=1,在△F MC中,由|FC|2=|F M|2+|MC|2得${({4-m})^2}={({2\sqrt{2}})^2}+{1^2}$,求出m,即可求实数a的值;
(2)根据对称性,结合以AB为直径的圆与圆C相切,求直线l的方程.
解答 解:(1)设焦点F(0,m),圆C:x2+(y-4)2=1,在△F MC中,
由|FC|2=|F M|2+|MC|2得${({4-m})^2}={({2\sqrt{2}})^2}+{1^2}$,
即4-m=±3,又m<3,解得m=1,即$a=\frac{1}{4}$.(5分)
(2)由(1)知x2=4y,圆C:x2+(y-4)2=1.
设直线l:y=kx+1.
由$\left\{\begin{array}{l}y=kx+1\\{x^2}=4y\end{array}\right.$得x2-4kx-4=0.
设 A(x1,y1),B(x2,y2),
则x1+x2=4k,x1x2=-4
所以$|{{A}{B}}|={y_1}+{y_2}+2=k({{x_1}+{x_2}})+4=4{k^2}+4$,A B中点Q(2k,2k2+1),
①若以A B为直径的圆与圆C内切,则$\sqrt{4{k^2}+{{({2{k^2}+1-4})}^2}}=2{k^2}+2-1$,
解得${k^2}=\frac{2}{3}$.直线l:$y=\frac{{\sqrt{6}}}{3}x+1$或$y=-\frac{{\sqrt{6}}}{3}x+1$.(10分)
②若以A B为直径的圆与圆C外切,则$\sqrt{4{k^2}+{{({2{k^2}+1-4})}^2}}=2{k^2}+2+1$,解得k=0.
所以直线l:y=1.
所以直线l:$y=\frac{{\sqrt{6}}}{3}x+1$或$y=-\frac{{\sqrt{6}}}{3}x+1$或y=1(12分)
点评 本题考查抛物线方程,考查圆与圆的位置关系,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
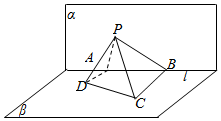 如图,已知平面α∩平面β=l,α⊥β,A,B是直线l上的两点,C,D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8,P是平面α内的一动点,使得直线CP,DP与平面α所成角相等,则三角形PAB面积的最大值为12.
如图,已知平面α∩平面β=l,α⊥β,A,B是直线l上的两点,C,D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8,P是平面α内的一动点,使得直线CP,DP与平面α所成角相等,则三角形PAB面积的最大值为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | [-1,3) | C. | [-1,+∞) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | 1或-5 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z的实部为$-\frac{1}{5}$ | B. | z的虚部为$-\frac{1}{5}i$ | ||
| C. | $|z|=\frac{3}{5}$ | D. | z的共轭复数为$\frac{3}{5}+\frac{1}{5}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com