
| A. | $\frac{7}{2}$ | B. | 4 | C. | 7 | D. | 8 |
分析 根据向量坐标分别求出向量长度和向量夹角,根据三角形的面积公式进行求解即可.
解答 解:∵$\overrightarrow{{A}{B}}$=(1,2),$\overrightarrow{{A}C}$=(-2,3),
∴|$\overrightarrow{{A}{B}}$|=$\sqrt{1+4}$=$\sqrt{5}$,|$\overrightarrow{{A}C}$|=$\sqrt{4+9}$=$\sqrt{13}$,
则cos<$\overrightarrow{{A}{B}}$,$\overrightarrow{{A}C}$>=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{-2+6}{\sqrt{5}•\sqrt{13}}$=$\frac{4}{\sqrt{65}}$,
则sinA=sin<$\overrightarrow{{A}{B}}$,$\overrightarrow{{A}C}$>=$\sqrt{1-(\frac{4}{\sqrt{65}})^{2}}$=$\frac{7}{\sqrt{65}}$,
在三角形的面积S=$\frac{1}{2}$AB•ACsinA=$\frac{1}{2}×\sqrt{5}×\sqrt{13}×\frac{7}{\sqrt{65}}$=$\frac{7}{2}$,
故选:A.
点评 本题主要考查三角形面积的计算,根据向量数量积求出向量长度和向量夹角,结合三角形的面积公式是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{π}{4}$,1) | B. | (2$\sqrt{2}$,$\frac{π}{4}$,1) | C. | (2,$\frac{5π}{4}$,1) | D. | (2$\sqrt{2}$,$\frac{5π}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{30}$ | B. | $\frac{13}{30}$ | C. | $\frac{11}{25}$ | D. | $\frac{13}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 28 | C. | 24 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
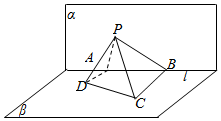 如图,已知平面α∩平面β=l,α⊥β,A,B是直线l上的两点,C,D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8,P是平面α内的一动点,使得直线CP,DP与平面α所成角相等,则三角形PAB面积的最大值为12.
如图,已知平面α∩平面β=l,α⊥β,A,B是直线l上的两点,C,D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8,P是平面α内的一动点,使得直线CP,DP与平面α所成角相等,则三角形PAB面积的最大值为12.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,1+\frac{{\sqrt{2}}}{2})$ | B. | $(1-\frac{{\sqrt{2}}}{2},1)$ | C. | $(1-\frac{{\sqrt{3}}}{2},1+\frac{{\sqrt{2}}}{2})$ | D. | $(1-\frac{{\sqrt{2}}}{2},1+\frac{{\sqrt{2}}}{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com