
���� ��1����t��x��=x2-lnx��x��[$\frac{1}{2}$��2]�����t��x���ķ�Χ��[$\frac{1+ln2}{2}$��4-ln2]��b��[1��3]ʱ����v��t��=|t-b|+2b+1����������ĵ����ԣ����M��b�����ɣ�
��2�������h��x���ĵ��������g��x���ı���ʽ����Ϻ����ĵ��������x0��ֵ���ɣ�
�����H��x����ֵ����y=$\frac{1}{2e}$x��[s��+�ޣ�������ֵ����[$\frac{s}{2e}$��+�ޣ�����s��e������y=$\frac{lnx}{x}$�ڣ�0��e��������[e��s���Ǽ���������ֵ���ǣ�-�ޣ�$\frac{1}{e}$]���õ�$\frac{s}{2e}$��$\frac{lns}{s}$����s2-2elns��0���٣���u��s��=s2-2elns�����ݺ����ĵ������жϼ��ɣ�
��� �⣺��1��F��x��=|x2-lnx-b|+2b+1��
��t��x��=x2-lnx��x��[$\frac{1}{2}$��2]����t�䣨x��=2x-$\frac{1}{x}$��
��t�䣨x��=0���ã�x=$\frac{\sqrt{2}}{2}$��
$\frac{1}{2}$��x��2ʱ��t�䣨x����0��t��x���ڣ�$\frac{1}{2}$��$\frac{\sqrt{2}}{2}$���ϵݼ���
$\frac{\sqrt{2}}{2}$��x��2ʱ��t�䣨x����0��t��x���ڣ�$\frac{\sqrt{2}}{2}$��2���ϵ�����
��t��$\frac{1}{2}$��=$\frac{1}{4}$+ln2��t��2��=4-ln2��t��$\frac{\sqrt{2}}{2}$��=$\frac{1+ln2}{2}$��t��2��-t��$\frac{1}{2}$��=$\frac{15}{4}$-2ln2��0��
��t��x���ķ�Χ��[$\frac{1+ln2}{2}$��4-ln2]��
b��[1��3]ʱ����v��t��=|t-b|+2b+1��
��v��t��=$\left\{\begin{array}{l}{-t+3b+1��\frac{1+ln2}{2}��t��b}\\{t+b+1��b��t��4-ln2}\end{array}\right.$��
��v��t����[$\frac{1+ln2}{2}$��b]�ϵݼ����ڣ�b��4-ln2]������
��v��$\frac{1+ln2}{2}$��=3b+$\frac{1-ln2}{2}$��v��4-ln2��=b+5-ln2��
v��$\frac{1+ln2}{2}$��-v��4-ln2��=2b+$\frac{ln2-9}{2}$��
��b��$\frac{9-ln2}{4}$ʱ�����ֵM��b��=v��4-ln2��=b+5-ln2��
b��$\frac{9-ln2}{4}$ʱ�����ֵM��b��=v��$\frac{1+ln2}{2}$��=3b+$\frac{1-ln2}{2}$��
��M��b��=$\left\{\begin{array}{l}{b+5-ln2��1��b��\frac{9-ln2}{4}}\\{3b+\frac{1-ln2}{2}��\frac{9-ln2}{4}��b��4}\end{array}\right.$��
��2��h��x��=$\frac{lnx}{x}$��
��h�䣨x��=$\frac{1-lnx}{{x}^{2}}$��h�䣨x0��=$\frac{1-l{nx}_{0}}{{{x}_{0}}^{2}}$��
��y��x��=$\frac{1-l{nx}_{0}}{{{x}_{0}}^{2}}$��x-x0��+y0��
g��x��=$\frac{lnx}{x}$-y0-$\frac{1-l{nx}_{0}}{{{x}_{0}}^{2}}$��x-x0����g��x0��=0��
g�䣨x��=$\frac{1-lnx}{{x}^{2}}$-$\frac{1-l{nx}_{0}}{{{x}_{0}}^{2}}$��g�䣨x0��=0��
��G��x��=g�䣨x��=$\frac{1-lnx}{{x}^{2}}$-$\frac{1-l{nx}_{0}}{{{x}_{0}}^{2}}$��G�䣨x��=$\frac{-3+2lnx}{{x}^{3}}$��
��g�䣨x���ڣ�0��${e}^{\frac{3}{2}}$���ݼ����ڣ�${e}^{\frac{3}{2}}$��+�ޣ�������
��x0��${e}^{\frac{3}{2}}$����x�ʣ�0��x0��ʱ��g�䣨x����0��g��x��������g��x����g��x0��=0��
x�ʣ�x0��${e}^{\frac{3}{2}}$��ʱ��g�䣨x����0��g��x���ݼ���g��x����g��x0��=0�����������⣬
��x0��${e}^{\frac{3}{2}}$����x�ʣ�${e}^{\frac{3}{2}}$��x0��ʱ��g�䣨x����0��g��x���ݼ���g��x����g��x0��=0��
x�ʣ�x0��+�ޣ�ʱ��g�䣨x����0��g��x��������g��x����g��x0��=0�����������⣬
��x0=${e}^{\frac{3}{2}}$����x�ʣ�0��${e}^{\frac{3}{2}}$��ʱ��g��x����0��x�ʣ�${e}^{\frac{3}{2}}$��+�ޣ�ʱ��g��x����0���������⣬
���ϣ�����x0����Ҫ����x0��ȡֵ������{${e}^{\frac{3}{2}}$}��
�ڡ߶�����ʵ��k���ܴ���ʵ��x0��ʹ��H��x0��=k������
��y=H��x����ֵ����R��
y=$\frac{1}{2e}$x��[s��+�ޣ�������ֵ����[$\frac{s}{2e}$��+�ޣ���
����y=$\frac{lnx}{x}$��y��=$\frac{1-lnx}{{x}^{2}}$��x=eʱ��y��=0��
x��eʱ��y�䣾0���ڣ�e��+�ޣ�������
0��x��eʱ��y�䣼0���ڣ�0��e���ݼ���
��s��e������y=$\frac{lnx}{x}$�ڣ�0��e��������[e��s���Ǽ�������
��ֵ���ǣ�-�ޣ�$\frac{1}{e}$]��
��$\frac{1}{e}$��$\frac{s}{2e}$�����������⣬��ȥ��
��0��s��e������y=$\frac{lnx}{x}$�ڣ�0��s��������
��ֵ���ǣ�-�ޣ�$\frac{lns}{s}$����
������ã�$\frac{s}{2e}$��$\frac{lns}{s}$����s2-2elns��0���٣�
��u��s��=s2-2elns��u�䣨s��=2s-$\frac{2e}{s}$=$\frac{2{��s}^{2}-e��}{s}$��
0��s��$\sqrt{e}$ʱ��u�䣨s����0��u��s���ڣ�0��$\sqrt{e}$���ݼ���
s��$\sqrt{e}$ʱ��u�䣨s����0��u��s���ڣ�$\sqrt{e}$��e��������
��s=$\sqrt{e}$ʱ��u��s������Сֵu��$\sqrt{e}$��=0��
�Ӷ�u��s����0����������ҽ���s=$\sqrt{e}$ʱ��u��s��=0���ڣ�
�ɢ٢ڵã�u��s��=0���ã�s=$\sqrt{e}$��
���ϣ�ʵ��s��ȡֵ������{$\sqrt{e}$}��
���� ���⿼���˺����ĵ����ԡ���ֵ���⣬���鵼����Ӧ���Լ�������������⣬�����������˼�룬ת��˼�룬��һ���ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | A��B=∅ | B�� | ��∁RA����B={x|x��0} | C�� | A��B={x|x��0} | D�� | ��∁RA����B={-2��-1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������һ����С��2 | B�� | ��С��2 | ||
| C�� | ������һ��������2 | D�� | ������2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
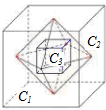 ��ͼ�����ⳤΪ1��������C1����C1�����������Ϊ�������������ΪC2����C2���������Ϊ�����������ΪC3����C3�����������Ϊ�������������ΪC4�������Դ����Ƶ�һϵ�еĶ�����Cn����Cn���ⳤΪan��������{an}�ĸ����Ϊ$\frac{6+3\sqrt{2}}{4}$��
��ͼ�����ⳤΪ1��������C1����C1�����������Ϊ�������������ΪC2����C2���������Ϊ�����������ΪC3����C3�����������Ϊ�������������ΪC4�������Դ����Ƶ�һϵ�еĶ�����Cn����Cn���ⳤΪan��������{an}�ĸ����Ϊ$\frac{6+3\sqrt{2}}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com