
���� ��1���������ַ��̵Ļ�������������д������C1�ļ����귽��������C2��ֱ�����귽�̣�
��2��$A��{��_1}���ȣ���B��{��_2}����+\frac{��}{2}��$�ֱ����$\frac{{{��^2}{{cos}^2}��}}{4}+{��^2}{sin^2}��=1$�У�������$\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OB}|}^2}}}$��ֵ��
��� �⣺��1��$\left\{\begin{array}{l}1=acos\frac{��}{3}\\ y=bsin\frac{��}{3}\end{array}\right.⇒\left\{\begin{array}{l}a=2\\ b=1\end{array}\right.⇒{C_1}��\frac{x^2}{4}+{y^2}=1$
���C1�ļ����귽��Ϊ$\frac{{{��^2}{{cos}^2}��}}{4}+{��^2}{sin^2}��=1$${C_2}��{x^2}+{y^2}=2y$
��2��M1��0��1����M2��2��0��⇒M1M2��x+2y-2=0
ǡ�ù�${C_2}��{x^2}+{y^2}=2y$��Բ�ģ���OP��OQ⇒OA��OB��
��$A��{��_1}���ȣ���B��{��_2}����+\frac{��}{2}��$
�ֱ����$\frac{{{��^2}{{cos}^2}��}}{4}+{��^2}{sin^2}��=1$�У�
��$\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OB}|}^2}}}=\frac{1}{��_1^2}+\frac{1}{��_2^2}=\frac{{{{cos}^2}��}}{4}+{sin^2}��+\frac{{{{sin}^2}��}}{4}+{cos^2}��=\frac{5}{4}$��
���� ���⿼�����ַ��̵Ļ��������鼫���귽�̵����ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 1 | C�� | $\frac{1}{16}$ | D�� | $\frac{1}{32}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\frac{3}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
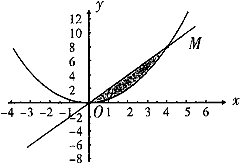 ������x2=2y���ԭ���ֱ���ཻ�ڵ�M����ֱ��OM����б��Ϊ�ȣ����߶�OM������Χ�ɵķ��ͼ�ε����S���ȣ���ͼ������ǣ�������
������x2=2y���ԭ���ֱ���ཻ�ڵ�M����ֱ��OM����б��Ϊ�ȣ����߶�OM������Χ�ɵķ��ͼ�ε����S���ȣ���ͼ������ǣ�������| A�� | 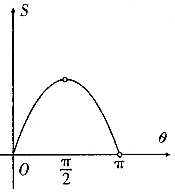 | B�� | 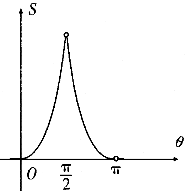 | ||
| C�� | 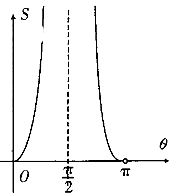 | D�� | 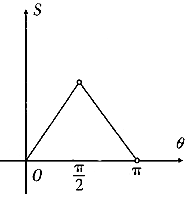 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
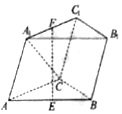 ��ͼ��������ABC-A1B1C1�У�����AA1C1C�͵���ACB��AA1=A1C=AC=2$\sqrt{3}$��BC=$\sqrt{3}$����A1C��BC����E��F�ֱ�ΪAB��A1C1���е㣮
��ͼ��������ABC-A1B1C1�У�����AA1C1C�͵���ACB��AA1=A1C=AC=2$\sqrt{3}$��BC=$\sqrt{3}$����A1C��BC����E��F�ֱ�ΪAB��A1C1���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com