
已知数列{an}的首项a1=2a+1(a是常数,且a≠-1),
an=2an-1+n2-4n+2(n≥2),数列{bn}的首项b1=a,
bn=an+n2(n≥2).
(1) 证明:{bn}从第2项起是以2为公比的等比数列;
(2) 设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;
(3) 当a>0时,求数列{an}的最小项.
(1) 证明:∵ bn=an+n2,∴ bn+1=an+1+(n+1)2=2an+(n+1)2-4(n+1)+2+(n+1)2=2an+2n2=2bn(n≥2).
由a1=2a+1,得a2=4a,b2=a2+4=4a+4,∵ a≠-1,
∴ b2≠0,即{bn}从第2项起是以2为公比的等比数列.
(2) 解:由(1)知bn=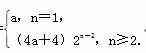
Sn=a+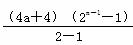 =-3a-4+(2a+2)2n,当n≥2时,
=-3a-4+(2a+2)2n,当n≥2时,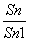 =
=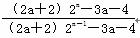
=2+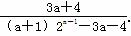 .
.
∵ {Sn}是等比数列, ∴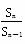 (n≥2)是常数,∴ 3a+4=0,即a=-
(n≥2)是常数,∴ 3a+4=0,即a=- .
.
(3) 解:由(1)知当n≥2时,bn=(4a+4)2n-2=(a+1)2n,
∴ an=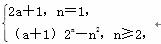
∴ 数列{an}为2a+1,4a,8a-1,16a,32a+7,…
显然最小项是前三项中的一项.
当a∈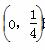 时,最小项为8a-1;
时,最小项为8a-1;
当a= 时,最小项为4a或8a-1;
时,最小项为4a或8a-1;
当a∈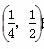 时,最小项为4a;
时,最小项为4a;
当a= 时,最小项为4a或2a+1;
时,最小项为4a或2a+1;
当a∈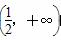 时,最小项为2a+1.
时,最小项为2a+1.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AC1、A1B1的中点.点 在正方体的表面上运动,则总能使
在正方体的表面上运动,则总能使 与
与 垂直的点
垂直的点 所构成的轨迹的周长等于 .
所构成的轨迹的周长等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
在数列{an}中,a1=2,an+1=4an-3n+1,n∈N*.
(1) 求证:数列{an-n}是等比数列;
(2) 求数列{an}的前n项和Sn;
(3) 求证:不等式Sn+1≤4Sn对任意n∈N*皆成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
水土流失是我国西部大开发中最突出的问题,全国9 100万亩坡度为25°以上的坡耕地需退耕还林,其中西部占70%,2002年国家确定在西部地区退耕还林面积为515万亩,以后每年退耕土地面积递增12%.
(1) 试问,从2002年起到哪一年西部地区基本上解决退耕还林问题?
(2) 为支持退耕还林工作,国家财政补助农民每亩300斤粮食,每斤粮食按0.7元计算,并且每亩退耕地每年补助20元,试问到西部地区基本解决退耕还林问题时,国家财政共需支付约多少亿元?
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,A、B、C所对的边分别是a、b、c,且bcosB是acosC、ccosA的等差中项.
(1) 求B的大小;
(2) 若a+c=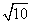 ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com