练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，A、B、C所对的边分别是a、b、c，且bcosB是acosC、ccosA的等差中项．

    (1) 求B的大小；

    (2) 若a＋c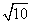＝，b＝2，求△ABC的面积．


    解：(1) 由题意，得acosC＋ccosA＝2bcosB.由正弦定理，得sinAcosC＋cosAsinC＝2sinBcosB，

    即sin(A＋C)＝2sinBcosB.

    ∵  A＋C＝π－B，0＜B＜π，

    ∴  sin(A＋C)＝sinB≠0.

    ∴  cosB＝，∴  B＝.

    ∴  S△ABC＝acsinB＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知数列{an}的首项a1＝2a＋1(a是常数，且a≠－1)，

    an＝2an－1＋n2－4n＋2(n≥2)，数列{bn}的首项b1＝a，

    bn＝an＋n2(n≥2)．

    (1) 证明：{bn}从第2项起是以2为公比的等比数列；

    (2) 设Sn为数列{bn}的前n项和，且{Sn}是等比数列，求实数a的值；

    (3) 当a>0时，求数列{an}的最小项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     甲、乙两大超市同时开业，第一年的全年销售额均为a万元，由于经营方式不同，甲超市前n年的总销售额为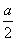(n2－n＋2)万元，乙超市第n年的销售额比前一年销售额多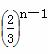a万元．

    (1) 设甲、乙两超市第n年的销售额分别为an、bn, 求an、bn的表达式；

    (2) 若其中某一超市的年销售额不足另一超市的年销售额的50%，则该超市将被另一超市收购，判断哪一超市有可能被收购？如果有这种情况，将会出现在第几年？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}，其前n项和为Sn.

    (1) 若对任意的n∈N，a2n－1，a2n＋1，a2n组成公差为4的等差数列，且a1＝1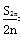，＝2 013，求n的值；

    (2) 若数列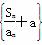是公比为q(q≠－1)的等比数列，a为常数，求证：数列{an}为等比数列的充要条件为q＝1＋.

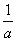    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，

    (1) 若a＝4，B＝30°，C＝105°，则b＝________．

    (2) 若b＝3，c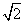＝，C＝45°，则a＝________．

    (3) 若AB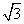＝，BC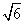＝，C＝30°，则∠A＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC中，∠B＝45°，AC＝4，则△ABC面积的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


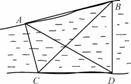
    如图，要测量河对岸A、B两点间的距离，今沿河岸选取相距40 m的C、D两点，测得∠ACB＝60°，∠BCD＝45°，∠ADB＝60°，∠ADC＝30°，则AB的距离是__________ m.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设△ABC的三个内角A、B、C所对的边分别是a、b、c，且则A＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     若cos＝，π＜x＜π，求的值．

    查看答案和解析>>

    同步练习册答案