
分析 (1)由已知结合$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$,可得x-α=$\frac{π}{3}$,再由$\overrightarrow a⊥\overrightarrow c$,结合坐标运算可得tan2α的值;
(2)写出函数$f(x)=\overrightarrow b•\overrightarrow c$,然后令$t=sinx+cosx(\frac{π}{4}<x<π)$换元,转化为关于t的一元二次函数求解.
解答 解:(1)由已知,$cos\frac{π}{3}=\frac{\vec a•\vec b}{|\vec a||\vec b|}=cosαcosx+sinαsinx=cos(x-α)$,
∵0<α<x<π,∴0<x-α<π,得$x-α=\frac{π}{3}$.
由$\vec a⊥\vec c$,得cosα(sinx+2sinα)+sinα(cosx+2cosα)=0,
即sin(x+α)+2sin2α=0,
由x-$α=\frac{π}{3}$,得x=$α+\frac{π}{3}$,
∴sin(2$α+\frac{π}{3}$)+2sin2α=0,得$\frac{5}{2}sin2α+\frac{\sqrt{3}}{2}cos2α=0$,
∴tan2α=$-\frac{\sqrt{3}}{5}$;
(2)f(x)=cosxsinx+2ssinαcosx+sinxcosx+2sinxcosα=$2sinxcosx+\sqrt{2}(sinx+cosx)$.
令$t=sinx+cosx(\frac{π}{4}<x<π)$,则$t∈(-1,\sqrt{2})$,
且2sinxcosx=t2-1,
∴$y={t^2}+\sqrt{2}t-1={(t+\frac{{\sqrt{2}}}{2})^2}-\frac{3}{2}$.
当$t=-\frac{{\sqrt{2}}}{2}$时,${y_{min}}=-\frac{3}{2}$,此时$sinx+cosx=-\frac{{\sqrt{2}}}{2}$,
即$\sqrt{2}sin(x+\frac{π}{4})=-\frac{{\sqrt{2}}}{2}⇒sin(x+\frac{π}{4})=-\frac{1}{2}$,
∵$\frac{π}{4}$<x<π,∴$\frac{π}{2}$<x+$\frac{π}{4}$<$\frac{5π}{4}$,得x+$\frac{π}{4}=\frac{7π}{6}$,x=$\frac{11π}{12}$.
∴f(x)的最小值为$-\frac{3}{2}$,相应的x的值为$\frac{11}{12}π$.
点评 本题考查平面向量的数量积运算,考查了数量积的坐标运算,训练了y=Asin(ωx+φ)型函数的性质应用,是中档题.


科目:高中数学 来源: 题型:填空题
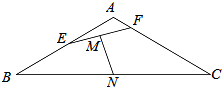 如图,等腰三角形ABC,AB=AC=2,∠BAC=120°.E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|MN|的最小值为$\frac{1}{2}$.
如图,等腰三角形ABC,AB=AC=2,∠BAC=120°.E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|MN|的最小值为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$,ω>0)的图象如图所示,函数$f(x)=g(x)+\frac{{\sqrt{3}}}{2}cos2x-\frac{3}{2}sin2x$
已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$,ω>0)的图象如图所示,函数$f(x)=g(x)+\frac{{\sqrt{3}}}{2}cos2x-\frac{3}{2}sin2x$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{10}$ | B. | $\frac{3}{10}$ | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com