
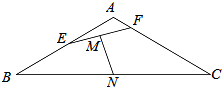
 如图,等腰三角形ABC,AB=AC=2,∠BAC=120°.E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|MN|的最小值为$\frac{1}{2}$.
如图,等腰三角形ABC,AB=AC=2,∠BAC=120°.E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|MN|的最小值为$\frac{1}{2}$. 分析 根据条件便可得到$\overrightarrow{MN}=\frac{1}{2}(1-m)\overrightarrow{AB}+\frac{1}{2}(1-n)\overrightarrow{AC}$,然后两边平方即可得出${\overrightarrow{MN}}^{2}=(1-m)^{2}+(1-n)^{2}-(1-m)(1-n)$,而由条件n=1-m,代入上式即可得出${\overrightarrow{MN}}^{2}=3{m}^{2}-3m+1$,从而配方即可求出${\overrightarrow{MN}}^{2}$的最小值,进而得出|MN|的最小值.
解答 解:$\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}$
=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})-\frac{1}{2}(m\overrightarrow{AB}+n\overrightarrow{AC})$
=$\frac{1}{2}(1-m)\overrightarrow{AB}+\frac{1}{2}(1-n)\overrightarrow{AC}$
∴${\overrightarrow{MN}}^{2}=\frac{1}{4}(1-m)^{2}{\overrightarrow{AB}}^{2}$$+\frac{1}{4}(1-n)^{2}{\overrightarrow{AC}}^{2}$$+\frac{1}{2}(1-m)(1-n)\overrightarrow{AB}•\overrightarrow{AC}$
=(1-m)2+(1-n)2-(1-m)(1-n);
∵m+n=1,∴n=1-m,代入上式得:
${\overrightarrow{MN}}^{2}=(1-m)^{2}+{m}^{2}+(1-m)m$
=3m2-3m+1
=$3(m-\frac{1}{2})^{2}+\frac{1}{4}$;
∵m∈(0,1);
∴$m=\frac{1}{2}$时,${\overrightarrow{MN}}^{2}$取最小值$\frac{1}{4}$;
∴|MN|的最小值为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 考查向量加法的平行四边形法则,向量减法的几何意义,向量的数乘运算,以及向量数量积的运算及计算公式,配方求二次函数最值的方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com