
分析 (1)利用余弦定理即可得出.
(2)利用余弦定理可得a=b,再利用三角形面积计算公式即可得出.
解答 解:(1)∵a2+b2+ab=c2.
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{-ab}{2ab}$=-$\frac{1}{2}$.
∵C∈(0,π),∴C=$\frac{2}{3}π$.
(2)∵c=2acosB,b=2,
∴c=2a×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
∴a2=b2,即a=b=2,
∴△ABC的面积S=$\frac{1}{2}$absinC=$\frac{1}{2}×{2}^{2}$×$sin\frac{2π}{3}$=$\sqrt{3}$.
点评 本题考查了余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:解答题
| 测试指标 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 产品A | 8 | 12 | 40 | 32 | 8 |
| 产品B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
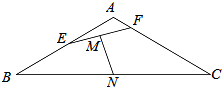 如图,等腰三角形ABC,AB=AC=2,∠BAC=120°.E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|MN|的最小值为$\frac{1}{2}$.
如图,等腰三角形ABC,AB=AC=2,∠BAC=120°.E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|MN|的最小值为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com