
分析 (1)利用两角和正弦公式化简函数f(x)的解析式,求出周期,由-1≤sin(x-$\frac{π}{3}$)≤1,求得函数f(x)的值域.
(2)利用正弦函数图象的性质来求函数的单调增区间.
解答 解:(1)∵$f(x)=\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx$
=cos$\frac{π}{3}$sinx-sin$\frac{π}{3}$cosx
=sin(x-$\frac{π}{3}$),
即f(x)=sin(x-$\frac{π}{3}$),
∴函数f(x)的最小正周期T=$\frac{2π}{1}$=2π,
又∵x∈R,
∴-1≤sin(x-$\frac{π}{3}$)≤1,
∴函数f(x)的值域为 {y|-1≤y≤1}.
(2)由2kπ-$\frac{π}{2}$≤x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,得2kπ-$\frac{π}{6}$≤x≤2kπ+$\frac{5π}{6}$,k∈Z,
∴函数f(x)的单调增区间为[2kπ-$\frac{π}{6}$,2kπ+$\frac{5π}{6}$](k∈Z).
点评 本题考查两角和正弦公式,正弦函数的单调性,周期性,和值域,化简函数f(x)的解析式,是解题的突破口.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| 身高x(cm) | 166 | 170 | 172 | 174 | 178 |
| 体重y(kg) | 55 | 60 | 65 | 65 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x0) | B. | -f′(x0) | C. | f(x0) | D. | -f(x0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
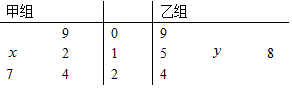 如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为5,乙组数据的平均数为6.8,则x,y的值分别为( )
如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为5,乙组数据的平均数为6.8,则x,y的值分别为( )| A. | 2,5 | B. | 5,5 | C. | 5,8 | D. | 8,8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数的单调区间可以是函数的定义域 | |
| B. | 函数的多个单调增区间的并集也是其单调增区间 | |
| C. | 具有奇偶性的函数的定义域定关于原点对称 | |
| D. | 关于原点对称的图象一定是奇函数的图象 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com