
分析 (1)分别计算潜入水底用时用氧量,水底作业时用氧量和返回水面用时用氧量,即可得到总用氧量的函数y;
(2)求导数y′,判断函数y的单调性,讨论c的取值,求出下潜速度v取什么值时消耗氧气的总量最少.
解答 解:(1)由题意,下潜用时$\frac{60}{v}$单位时间,
用氧量为[${(\frac{v}{10})}^{3}$+1]×$\frac{60}{v}$=$\frac{{3v}^{2}}{50}$+$\frac{60}{v}$(升),
水底作业时的用氧量为10×0.9=9(升),
返回水面用时$\frac{60}{\frac{v}{2}}$=$\frac{120}{v}$单位时间,
用氧量为$\frac{120}{v}$×1.5=$\frac{180}{v}$(升),
∴总用氧量为y=$\frac{{3v}^{2}}{50}$+$\frac{240}{v}$+9(v>0);
(2)求导数y′=$\frac{6v}{50}$-$\frac{240}{{v}^{2}}$=$\frac{3{(v}^{3}-2000)}{2{5v}^{2}}$,
令y'=0,解得v=10$\root{3}{2}$,
在0<v<10$\root{3}{2}$时,y'<0,函数y单调递减,
在v>10$\root{3}{2}$时,y'>0,函数y单调递增;
∴当c<10$\root{3}{2}$时,函数y在(0,10$\root{3}{2}$)上递减,在(10,$\root{3}{2}$15)上递增,
此时v=10$\root{3}{2}$时用氧量最少;
当c≥10$\root{3}{2}$时,函数y在[c,15]上递增,
此时v=c时,总用氧量最少.
点评 本题考查了函数模型的构建以及基本不等式的运用问题,也考查了利用导数判断函数单调性问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
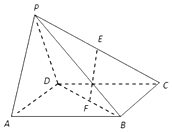 底面是正方形的四棱锥中P-ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,若存在,请求出点G的位置;若不存在,请说明理由.
底面是正方形的四棱锥中P-ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,若存在,请求出点G的位置;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
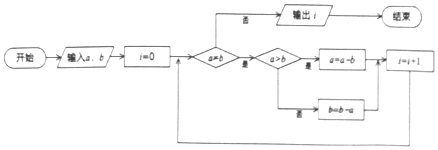
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com