
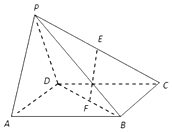
 底面是正方形的四棱锥中P-ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,若存在,请求出点G的位置;若不存在,请说明理由.
底面是正方形的四棱锥中P-ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,若存在,请求出点G的位置;若不存在,请说明理由. 分析 取AD中点O,连结PO,以O为原点,OA为x轴,在平面ABCD中过O作AD的垂线为y轴,以OP为z轴,建立空间直角坐标系,利用向量法求出在线段AB上存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,且AG=$\frac{2\sqrt{3}}{3}$.
解答 解: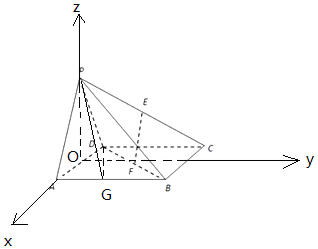 假设在线段AB上存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$.
假设在线段AB上存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$.
取AD中点O,连结PO,
∵底面是正方形的四棱锥中P-ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,
∴PO⊥平面ABCD,
以O为原点,OA为x轴,在平面ABCD中过O作AD的垂线为y轴,以OP为z轴,
建立空间直角坐标系,设PA=PD=$\sqrt{2}$,
则G(1,t,0)(0≤t≤2),C(-1,2,0),P(0,0,$\sqrt{2}$),D(-1,0,0),
$\overrightarrow{PD}$=(-1,0,-$\sqrt{2}$),$\overrightarrow{PC}$=(-1,2,-$\sqrt{2}$),$\overrightarrow{PG}$=(1,t,-$\sqrt{2}$),
设平面PCD的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PD}=-x-\sqrt{2}z=0}\\{\overrightarrow{n}•\overrightarrow{PC}=-x+2y-\sqrt{2}z=0}\end{array}\right.$,取x=$\sqrt{2}$,得$\overrightarrow{n}$=($\sqrt{2}$,0,-1),
设平面PDG的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PD}=-a-\sqrt{2}c=0}\\{\overrightarrow{m}•\overrightarrow{PG}=a+tb-\sqrt{2}c=0}\end{array}\right.$,取a=$\sqrt{2}$,得$\overrightarrow{m}$=($\sqrt{2}$,-$\frac{2\sqrt{2}}{t}$,-1),
∵二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,
∴$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{3}{\sqrt{3}×\sqrt{3+\frac{8}{{t}^{2}}}}$=$\frac{\sqrt{3}}{3}$,解得t=$\frac{2\sqrt{3}}{3}$,
∴在线段AB上存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,且AG=$\frac{2\sqrt{3}}{3}$.
点评 本题考查满足条件的点的位置的确定与求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
 全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:
全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3)区间 | [0,50) | [50,100) | [100,150) | [150,200) | [200,250) |
| 空间质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com