
分析 先利用正三棱锥的特点,将球的内接三棱锥问题转化为球的内接正方体问题,从而将所求距离转化为正方体中,中心到截面的距离问题,利用等体积法可实现此计算.
解答 解:∵正三棱锥P-ABC,PA,PB,PC两两垂直,
∴此正三棱锥的外接球即以PA,PB,PC为三边的正方体的外接球O,
∵球O的半径为3,
∴正方体的边长为2$\sqrt{3}$,即PA=PB=PC=2$\sqrt{3}$,
球心到截面ABC的距离即正方体中心到截面ABC的距离,
设P到截面ABC的距离为h,则正三棱锥P-ABC的体积V=$\frac{1}{3}$S△ABC×h=$\frac{1}{3}$S△PAB×PC=4$\sqrt{3}$,
△ABC为边长为2$\sqrt{6}$的正三角形,S△ABC=6$\sqrt{3}$
∴h=2,
∴球心(即正方体中心)O到截面ABC的距离:3-2=1.
故答案为1.
点评 本题主要考球的内接三棱锥和内接正方体间的关系及其相互转化,棱柱的几何特征,球的几何特征,点到面的距离问题的解决技巧,有一定难度,属中档题.


科目:高中数学 来源: 题型:解答题
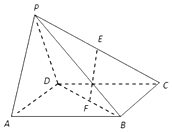 底面是正方形的四棱锥中P-ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,若存在,请求出点G的位置;若不存在,请说明理由.
底面是正方形的四棱锥中P-ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,若存在,请求出点G的位置;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}\overrightarrow{AB}-\frac{3}{4}\overrightarrow{AC}$ | B. | $\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$ | C. | $\frac{3}{4}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AC}$ | D. | $\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com