
分析 (Ⅰ)根据正弦定理和两角和的正弦公式和三角形的面积公式即可求出,
(Ⅱ)设BD=x,由余弦定理求出x的值,再根据勾股定理即可求出.
解答 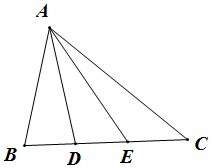 解:(Ⅰ)B=60°,c=4,b=6,
解:(Ⅰ)B=60°,c=4,b=6,
在△ABC中,由正弦定理$\frac{b}{sinB}=\frac{c}{sinC}$,
得$sinC=\frac{csinB}{b}=\frac{{4•\frac{{\sqrt{3}}}{2}}}{6}=\frac{{\sqrt{3}}}{3}$,
又b>c,所以B>C,则C为锐角,所以$cosC=\frac{{\sqrt{6}}}{3}$,
则sinA=sin(B+C)=sinBcosC+cosBsinC=$\frac{{\sqrt{3}}}{2}•\frac{{\sqrt{6}}}{3}+\frac{1}{2}•\frac{{\sqrt{3}}}{3}=\frac{{3\sqrt{2}+\sqrt{3}}}{6}$,
所以△ABC的面积$S=\frac{1}{2}bcsinA=12•\frac{{3\sqrt{2}+\sqrt{3}}}{6}=6\sqrt{2}+2\sqrt{3}$.
(Ⅱ)设BD=x,则BE=2x,$AE=2\sqrt{3}x$,又B=60°,c=4,
在△ABE中,由余弦定理得12x2=16+4x2-2•4•2x•cos60°,
即8x2=16-8x,解得x=1,
则BE=2,所以∠AEB=90°,
在直角△ADE中,$AD=\sqrt{A{E^2}+D{E^2}}=\sqrt{12+1}=\sqrt{13}$.
点评 本题考查了正弦定理和余弦定理和三角形的面积公式和两角和的正弦公式,考查了学生的运算能力和分析解决问题的能力,属于中档题


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
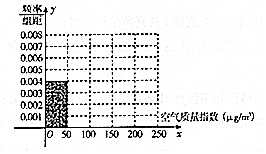 全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:
全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3)区间 | [0,50) | [50,100) | [100,150) | [150,200) | [200,250) |
| 空间质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 △ABC的内角A,B,C的对边分别为a,b,c,其中b≠c,
△ABC的内角A,B,C的对边分别为a,b,c,其中b≠c,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com