
 全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:
全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3)区间 | [0,50) | [50,100) | [100,150) | [150,200) | [200,250) |
| 空间质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
分析 (1)利用统计表和频率分布直方图能求出n,m的值,并能完成频率分布直方图.
(2)由频率分布直方图能求出该组数据的平均数和中位数.
(3)空气质量指数为[50,100)和[150,200)的监测天数中分布抽取4天和1天,在所抽取的5天中,将空气质量指数为[50,100)的4天分别记为a,b,c,d,将空气质量指数为[150,200)的1天记为e.从中任取2天,利用列举法能求出事件A”两天空气都为良“发生的概率.
解答 解:(1)∵0.004×50=$\frac{2}{n}$,解得n=100,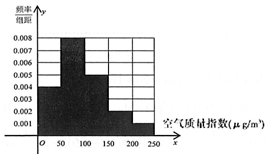
∵20+40+m+10+5=100,解得m=25,
$\frac{40}{100×50}$=0.008,$\frac{25}{100×50}=0.005$,$\frac{10}{100×50}=0.002$,$\frac{5}{100×50}=0.001$.
完成频率分布直方图如右图:
(2)由频率分布直方图知该组数据的平均数为:
$\overline{x}$=25×0.004×50+75×0.008×50+125×0.005×50+
175×0.002×50+225×0.001×50=95.
∵[0,50)的频率为0.004×50=0.2,[50,100)的频率为0.008×50=0.4,
∴该组数据的中位数为:$50+\frac{0.5-0.2}{0.4}×50$=87.5.
(3)空气质量指数为[50,100)和[150,200)的监测天数中分布抽取4天和1天,
在所抽取的5天中,将空气质量指数为[50,100)的4天分别记为a,b,c,d,
将空气质量指数为[150,200)的1天记为e.
从中任取2天的基本事件分别为:
(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e),共10天,
基其中事件A“两天空气都为良”包含的基本事件为:
(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),共6天,
∴事件A”两天空气都为良“发生的概率P(A)=$\frac{6}{10}=\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想、数形结合思想,是基础题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\;1,\;\;\frac{π}{2})$ | B. | (1,0) | C. | $(\;\frac{1}{2},\;\;\frac{π}{2}\;)$ | D. | $(\;\frac{1}{2},\;\;0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
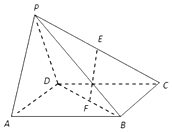 底面是正方形的四棱锥中P-ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,若存在,请求出点G的位置;若不存在,请说明理由.
底面是正方形的四棱锥中P-ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$,若存在,请求出点G的位置;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com