
分析 (1)直接利用三角函数的图象和性质求解.
(2)将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;
解答 解:(1)由题意已知f(x)=3sin2x.
∴函数f(x)的最小值周期为$T=\frac{2π}{2}=π$,
由正弦函数图象及性质,可知:
当2x=$\frac{π}{2}$+2kπ(k∈Z)f(x)取得最大值,即fmax(x)=f($\frac{π}{2}$)=3sin$\frac{π}{2}$=3.
(2)由正弦函数图象及性质可得:
$-\frac{π}{2}+2kπ≤2x≤\frac{π}{2}+2kπ,k∈Z$是单调增区间,
解得:$-\frac{π}{4}+kπ≤x≤\frac{π}{4}+kπ,k∈Z$
所以:f(x)的单调递增区间是$[-\frac{π}{4}+kπ,\frac{π}{4}+kπ],k∈Z$.
点评 本题考查了正弦函数的图象及性质的运用.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
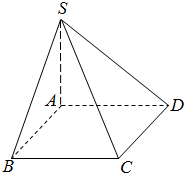 如图,四棱锥S-ABCD的底面为正方形,SA⊥底面ABCD,且SA=AD,则异面直线DC与SB所成的角为( )
如图,四棱锥S-ABCD的底面为正方形,SA⊥底面ABCD,且SA=AD,则异面直线DC与SB所成的角为( )| A. | 60° | B. | 30° | C. | 45° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(文)试卷(解析版) 题型:选择题
已知命题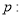 对任意
对任意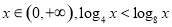 ,命题
,命题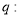 存在
存在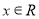 ,使得
,使得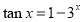 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )
A.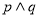 B.
B.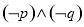 C.
C.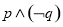 D.
D.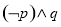
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com