
| A. | (4,8) | B. | (4,3$\sqrt{7}$) | C. | ($\sqrt{15}$,3$\sqrt{7}$) | D. | ($\sqrt{15}$,8) |
分析 根据对函数的解析式进行变形后发现当x∈(-1,1],[3,5],[7,9]上时,f(x)的图象为半个椭圆.根据图象推断要使方程恰有5个实数解,则需直线y=x与第二个椭圆相交,而与第三个椭圆无公共点.把直线分别代入椭圆方程,根据△可求得λ的范围
解答 解:∵当x∈(-1,1]时,将函数化为方程x2+$\frac{{y}^{2}}{{λ}^{2}}$=1(y≥0),
∴实质上为一个半椭圆,
当x∈(1,3]时,f(x)=3-3|x-2|是一段折线,
其图象如图所示,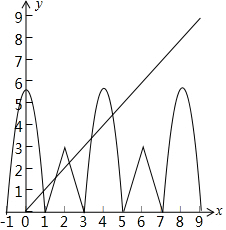
同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,
由图易知直线y=x与第二个半椭圆(x-4)2+$\frac{{y}^{2}}{{λ}^{2}}$=1(y≥0)相交,
但与第三个半椭圆(x-8)2+$\frac{{y}^{2}}{{λ}^{2}}$=1无公共点时,方程恰有5个实数解,
将y=x代入(x-4)2+$\frac{{y}^{2}}{{λ}^{2}}$=1 (y≥0)得,
(1+$\frac{1}{{λ}^{2}}$)x2-8x+15=0,由△=64-60 (1+$\frac{1}{{λ}^{2}}$)>0,得λ2>15,且λ>0得λ>$\sqrt{15}$,
将y=x代入(x-8)2+$\frac{{y}^{2}}{{λ}^{2}}$=1(y≥0)得,
(1+$\frac{1}{{λ}^{2}}$)x2-16x+63=0,由△=256-252 (1+$\frac{1}{{λ}^{2}}$)<0,得λ2<63,且λ>0得:0<λ<$3\sqrt{7}$,
综上可知m∈($\sqrt{15}$,3$\sqrt{7}$)
故选:C
点评 本题主要考查了函数的周期性.采用了数形结合的方法,很直观.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
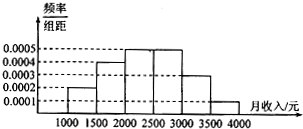 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图所示).为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2000,2500]月收入段应抽出( )
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图所示).为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2000,2500]月收入段应抽出( )| A. | 10人 | B. | 15人 | C. | 20人 | D. | 25人 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\sqrt{3},\sqrt{3}]$ | B. | $(\sqrt{3},2\sqrt{3}]$ | C. | (1,2] | D. | $(\frac{{\sqrt{3}}}{2},\sqrt{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{4}$,1) | B. | [$\frac{5}{7}$,1) | C. | [$\frac{9}{10}$,1) | D. | [$\frac{5}{7}$,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com