
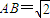 ,是否存在点E满足EF与平面FA1C1所成角为
,是否存在点E满足EF与平面FA1C1所成角为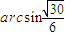 ,若存在,求点E到平面A1C1CA的距离;若不存在,说明理由.
,若存在,求点E到平面A1C1CA的距离;若不存在,说明理由.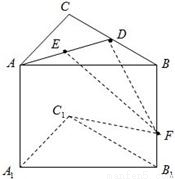
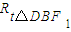 ≌
≌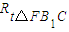 证明C1F⊥FD,可得C1F⊥面DEF;即可得证;
证明C1F⊥FD,可得C1F⊥面DEF;即可得证;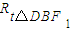 ≌
≌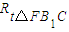 ,∴∠DBF+∠C1FB1=
,∴∠DBF+∠C1FB1=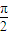 ,
,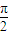 ∴C1F⊥FD,
∴C1F⊥FD,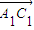 =(0,
=(0,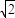 ,0),
,0),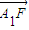 =(
=(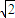 ,0,1),
,0,1),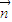 =(x,y,z),则有
=(x,y,z),则有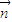
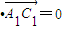 ,
,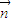
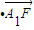 =0可得
=0可得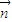 =(1,0,-
=(1,0,-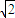 ),D(
),D(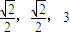 )
)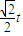 ,
,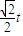 ,3)(0<t<1),
,3)(0<t<1),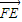 =(
=(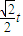 -
-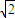 ,
,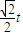 ,2),由已知
,2),由已知 =
=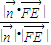 .
.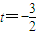 或t=1
或t=1

 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:
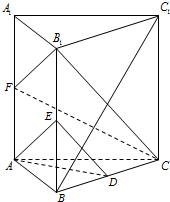 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.A1Q=3QA, BC=
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.A1Q=3QA, BC=| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com