Question

11．半径为2的球面上有三点A，B，C，满足$AB=2\sqrt{3}，BC=2，AC=2\sqrt{2}$，若P为球面上任意一点，则三棱锥P-ABC体积的最大值为$2\sqrt{2}$．

Answer 1

分析 由题意画出图形，可知△ABC为球内接直角三角形，连接三角形外接圆的圆心与球心交球于P，求出三棱锥的高，则三棱锥P-ABC体积的最大值可求．

解答 解：如图，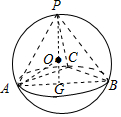

∵$AB=2\sqrt{3}，BC=2，AC=2\sqrt{2}$，
∴AC⊥BC，设球心为O，AB的中点为G，连接GO并延长交球于P，
此时三棱锥P-ABC体积的最大，
连接OA，在Rt△OGA中，则OG=$\sqrt{O{A}^{2}-A{G}^{2}}=\sqrt{{2}^{2}-（\sqrt{3}）^{2}}=1$．
则PG=3，
∴三棱锥P-ABC体积的最大值为V=$\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×2×3=2\sqrt{2}$．
故答案为：$2\sqrt{2}$．

点评 本题考查棱柱、棱锥、棱台体积的求法，考查了空间想象能力和思维能力，是中档题．