
(2014•南昌模拟)过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则△AOB的面积为( )
A.5 B.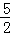 C.
C.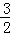 D.
D.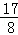
B
【解析】
试题分析:设A(x1,y1)、B(x2,y2),算出抛物线的焦点坐标,从而可设直线AB的方程为y=k(x﹣1),与抛物线方程联解消去x可得y2﹣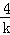 y﹣4=0,利用根与系数的关系算出y1y2=﹣4.根据|AF|=5利用抛物线的抛物线的定义算出x1=4,可得y1=±4,进而算出|y1﹣y2|=5,最后利用三角形的面积公式加以计算,即可得到△AOB的面积.
y﹣4=0,利用根与系数的关系算出y1y2=﹣4.根据|AF|=5利用抛物线的抛物线的定义算出x1=4,可得y1=±4,进而算出|y1﹣y2|=5,最后利用三角形的面积公式加以计算,即可得到△AOB的面积.
【解析】
根据题意,抛物线y2=4x的焦点为F(1,0).
设直线AB的斜率为k,可得直线AB的方程为y=k(x﹣1),
由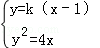 消去x,得y2﹣
消去x,得y2﹣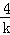 y﹣4=0,
y﹣4=0,
设A(x1,y1)、B(x2,y2),由根与系数的关系可得y1y2=﹣4.
根据抛物线的定义,得|AF|=x1+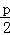 =x1+1=5,解得x1=4,
=x1+1=5,解得x1=4,
代入抛物线方程得:y12=4×4=16,解得y1=±4,
∵当y1=4时,由y1y2=﹣4得y2=﹣1;当y1=﹣4时,由y1y2=﹣4得y2=1,
∴|y1﹣y2|=5,即AB两点纵坐标差的绝对值等于5.
因此△AOB的面积为:
S=△AOB=S△AOF+S△BOF=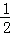 |OF|•|y1|+
|OF|•|y1|+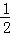 |OF|•|y2|=
|OF|•|y2|=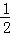 |OF|•|y1﹣y2|=
|OF|•|y1﹣y2|=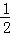 ×1×5=
×1×5=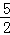 .
.
故选:B


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
若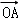 、
、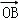 、
、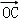 是空间不共面的三个向量,则与向量
是空间不共面的三个向量,则与向量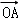 +
+ 和向量
和向量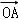 ﹣
﹣ 构成不共面的向量是( )
构成不共面的向量是( )
A.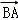 B.
B.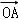 C.
C. D.
D.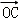
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
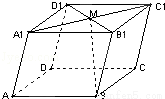
如图:在平行六面体ABCD﹣A1B1C1D1中,M为A1C1与B1D1的交点.若 ,
, ,
, ,则下列向量中与
,则下列向量中与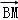 相等的向量是( )
相等的向量是( )
A.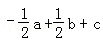 B.
B.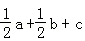 C.
C.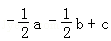 D.
D.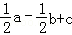
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 2.4圆锥曲线的应用练习卷(解析版) 题型:?????
(2014•长葛市三模)已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线l,此直线与上述两曲线的四个交点,自左向右顺次记为A,B,C,D,如果线段AB,BC,CD的长按此顺序构成一个等差数列,则直线l的斜率为( )
A.±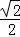 B.
B. C.±
C.± D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 2.4圆锥曲线的应用练习卷(解析版) 题型:?????
(2014•红桥区一模)若双曲线mx2+ny2=1的一个焦点与抛物线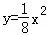 的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
A.y2+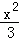 =1 B.y2﹣
=1 B.y2﹣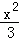 =1 C.
=1 C.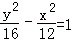 D.
D.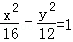
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 7.4副数的几何表示练习卷(解析版) 题型:?????
(2014•潍坊模拟)在复平面内,设z=1+i(i是虚数单位),则复数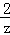 +z2对应的点位于( )
+z2对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 7.3复数的四则运算练习卷(解析版) 题型:?????
(2014•湖北)i为虚数单位,(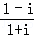 )2=( )
)2=( )
A.1 B.﹣1 C.i D.﹣i
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 7.1解方程与数系的扩充练习卷(解析版) 题型:?????
(2005•温州一模)用i表示虚数单位,则1+i+i2+…+i2005=( )
A.0 B.1 C.i D.1+i
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com