
【题目】若直线l1:y=x+a和直线l2:y=x+b将圆(x﹣1)2+(y﹣2)2=8分成长度相等的四段弧,则a2+b2= .
【答案】18
【解析】解:∵直线l1:y=x+a和直线l2:y=x+b为平行线,
∴若直线l1:y=x+a和直线l2:y=x+b将圆(x﹣1)2+(y﹣2)2=8分成长度相等的四段弧,
则圆心为C(1,2),半径为 ![]() =2
=2 ![]() ,
,
则圆心C到直线l1:y=x+a或l2:y=x+b的距离相等,且为2,
即d= ![]() =
= ![]() =2,
=2,
即|a﹣1|=2 ![]() ,
,
则a=2 ![]() +1或a=1﹣2
+1或a=1﹣2 ![]() ,
,
即a=2 ![]() +1,b=1﹣2
+1,b=1﹣2 ![]() 或b=2
或b=2 ![]() +1,a=1﹣2
+1,a=1﹣2 ![]() ,
,
则a2+b2=(2 ![]() +1)2+(1﹣2
+1)2+(1﹣2 ![]() )2=9+4
)2=9+4 ![]() +9﹣4
+9﹣4 ![]() =18,
=18,
故答案为:18
根据直线将圆分成长度相等的四段弧,转化为圆心C到直线l1:y=x+a或l2:y=x+b的距离相等,且为2,利用点到直线的距离公式进行求解即可.


科目:高中数学 来源: 题型:
【题目】设m,n是两条不同的直线,α、β是两个不同的平面,则下列命题不正确的是________.
(1).若m⊥n,m⊥α,n![]() α,则n∥α
α,则n∥α
(2).若m⊥β,α⊥β,则m∥α或m![]() α
α
(3).若m⊥n,m⊥α,n⊥β,则α⊥β
(4).若![]() ∥α,α⊥β,则
∥α,α⊥β,则![]() ⊥β
⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M是棱长为2的正方体的棱AD的中点,P是平面![]() 内一点,若面
内一点,若面![]() 分别与面ABCD和面
分别与面ABCD和面![]() 所成的锐二面角相等,则
所成的锐二面角相等,则![]() 长度的最小值是( )
长度的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn , a1=1,an+1=2Sn+1(n≥1).
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn , 且T3=15,又a1+b1 , a2+b2 , a3+b3成等比数列,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,地面上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高为10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧. 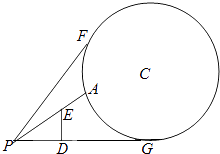
(1)若圆形标志物半径为25m,以PG所在直线为x轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即∠APF)的正切值为 ![]() ,求该圆形标志物的半径.
,求该圆形标志物的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
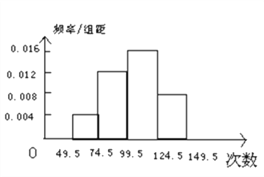
【题目】为了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图(如图所示),已知图中从左到右前三个小组的频率分别时0.1,0.3,0.4,第一小组的频数为5.
(1)求第四小组的频率?
(2)问参加这次测试的学生人数是多少?
(3)问在这次测试中,学生跳绳次数的中位数落在第几小组内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com