【题目】已知椭圆
的中心在坐标原点
，其焦点与双曲线
的焦点重合，且椭圆的短轴的两个端点与其一个焦点构成正三角形.
（1）求椭圆的方程；
（2）过双曲线
的右顶点
作直线
与椭圆交于不同的两点
.设
，当
为定值时，求
的值；
科目：高中数学 来源： 题型：
【题目】已如椭圆
的左、右焦点分别为
、
，
为
上的动点．
（1）若
，设点的横坐标为
，试用解析式将
表示成的函数；
（2）试根据
的不同取值，讨论满足
为等腰锐角三角形的点的个数．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法错误的是（ ）
A.若样本
的平均数为5，标准差为1，则样本
的平均数为11，标准差为2
B.身高和体重具有相关关系
C.现有高一学生30名，高二学生40名，高三学生30名，若按分层抽样从中抽取20名学生，则抽取高三学生6名
D.两个变量间的线性相关性越强，则相关系数的值越大
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下面类比推理：
①“若2a<2b，则a<b”类比推出“若a2<b2，则a<b”；
②“(a＋b)c＝ac＋bc(c≠0)”类比推出“
(c≠0)”；
③“a，b∈R，若a－b＝0，则a＝b”类比推出“a，b∈C，若a－b＝0，则a＝b”；
④“a，b∈R，若a－b>0，则a>b”类比推出“a，b∈C，若a－b>0，则a>b(C为复数集)”．
其中结论正确的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A，B，C，求：
(1)P(A)，P(B)，P(C).
(2)1张奖券的中奖概率.
(3)1张奖券不中特等奖，且不中一等奖的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2
。
（1）求椭圆的方程；
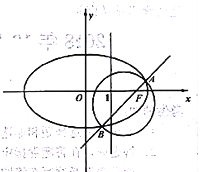
（2）如图，斜率为k的直线l过椭圆的右焦点F，且与椭圆交与A，B两点，以线段AB为直径的圆截直线x＝1所得的弦的长度为
，求直线l的方程。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）一个盒子里装有三张卡片，分别标记有数字
，
，
，这三张卡片除标记的数字外完全相同。随机有放回地抽取次，每次抽取张，将抽取的卡片上的数字依次记为
，
，
.
（Ⅰ）求“抽取的卡片上的数字满足
”的概率；
（Ⅱ）求“抽取的卡片上的数字，，不完全相同”的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了调查某校高二学生的身高是否与性别有关，随机调查该校64名高二学生，得到2×2列联表如表：
男生 | 女生 | 总计 | |
身高低于170cm | 8 | 24 | 32 |
身高不低于170cm | 26 | 6 | 32 |
总计 | 34 | 30 | 64 |
附：K2
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
由此得出的正确结论是（ ）
A.在犯错误的概率不超过0.01的前提下，认为“身高与性别无关”
B.在犯错误的概率不超过0.01的前提下，认为“身高与性别有关”
C.有99.9%的把握认为“身高与性别无关”
D.有99.9%的把握认为“身高与性别有关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
