练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．分配4名煤气工去3个不同的居民家里检查煤气管道，要求4名煤气工都分配出去，并每名煤气工只去一个居民家，且每个居民家都要有人去检查，那么分配的方案共有（　　）
    A．24种B．18种C．72种D．36种

    分析 根据题意，分析可得，必有2名煤气工去同一居民家检查；分两步进行，①先从4名煤气工中抽取2人，②再将这2人当做一个元素，与其他2人，共3个元素，分别分配到3个不同的居民家里，由分步计数原理，计算可得答案

    解答 解：根据题意，分配4名煤气工去3个不同的居民家里，要求4名煤气工都分配出去，且每个居民家都要有人去检查；
    则必有2名煤气工去同一居民家检查，
    即要先从4名煤气工中抽取2人，有C42种方法，
    再将这2人当做一个元素，与其他2人，共3个元素，分别分配到3个不同的居民家里，有A33种情况，
    由分步计数原理，可得共C42A33种不同分配方案，
    故选：D

    点评 本题考查排列、组合的综合应用，注意一般顺序是先分组（组合），再排列，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．△ABC在内角A、B、C所对的边分别为a，b，c；向量$\overrightarrow{m}$=（cosA，a）与$\overrightarrow{n}$=（sinB，$\sqrt{3}$b）平行．
    （1）求A；
    （2）若$a=\sqrt{7}，b=2$，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

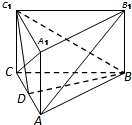    13．如图，在正三棱柱（侧棱垂直于底面，且底面是正三角形）ABC-A1B1C1中，D是AC边的中点．
    （1）求证：AB1∥平面DBC1；
    （2）当CA1⊥AB1时，求证：CA1⊥平面DBC1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知{an}是等差数列，且a3+a5+a7+a9=18，则a5+a7=（　　）
    A．12B．11C．9D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

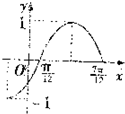    17．将函数y=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象向左平移$\frac{π}{12}$个单位长度后，所得曲线的一部分如图所示，则ω，φ的值分别为（　　）
    A．1，$\frac{π}{6}$B．1，$-\frac{π}{6}$C．2，$\frac{π}{3}$D．2，$-\frac{π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．设函数f（x）=lnx-$\frac{1}{2}$x2+1（x＞0），则下列关于函数y=f（x）的说法正确的是①（填序号）．
    ①在区间（0，1），（1，2）内均有零点；
    ②在区间（0，1）内有零点，在区间（1，2）内无零点；
    ③在区间（0，1），（1，2）内均无零点，；
    ④在区间（0，1）内无零点，在区间（1，2）内有零点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知log2m=$\frac{-1}{lo{g}_{2}3}$，则log2m=log3$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．在△ABC中，A，B，C所对的边分别是a，b，c，2cos（A+B）=1，且a，b 是方程x2-2$\sqrt{3}$x+2=0的两根．
    （1）求角C的度数；      
    （2）求AB的长；    
    （3）求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知函数f（x）的定义域为R，且f（1-x）=f（1+x），若f（-1）+f（3）=12，则f（3）=6．

    查看答案和解析>>

    同步练习册答案