
【题目】在数列![]() 中,已知
中,已知![]() ,且对于任意正整数n都有
,且对于任意正整数n都有![]() .
.
(1)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)求![]() 的通项公式;
的通项公式;
(3)设![]() 是一个正数,无论
是一个正数,无论![]() 为何值,都有一个正整数
为何值,都有一个正整数![]() 使
使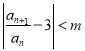 成立.
成立.
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两个同学分別抛掷一枚质地均匀的骰子.
(1)求他们抛掷的骰子向上的点数之和是4的倍数的概率;
(2)求甲抛掷的骰子向上的点数不大于乙抛掷的骰子向上的点数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.![]() 年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本
年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本![]() 万元,每生产
万元,每生产![]() (百辆),需另投入成本
(百辆),需另投入成本![]() 万元,且
万元,且 .由市场调研知,每辆车售价
.由市场调研知,每辆车售价![]() 万元,且全年内生产的车辆当年能全部销售完.
万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (百辆)的函数关系式;(利润=销售额-成本)
(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击运动员每次击中目标的概率是![]() ,在某次训练中,他只有4发子弹,并向某一目标射击.
,在某次训练中,他只有4发子弹,并向某一目标射击.
(1)若4发子弹全打光,求他击中目标次数![]() 的数学期望;
的数学期望;
(2)若他击中目标或子弹打光就停止射击,求消耗的子弹数![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( ) 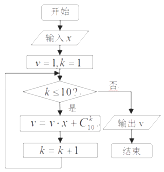
A.210﹣1
B.210
C.310﹣1
D.310
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高二年级一个学习兴趣小组进行社会实践活动,决定对某“著名品牌”![]() 系列进行市场销售量调研,通过对该品牌的
系列进行市场销售量调研,通过对该品牌的![]() 系列一个阶段的调研得知,发现
系列一个阶段的调研得知,发现![]() 系列每日的销售量
系列每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (元/千克)近似满足关系式
(元/千克)近似满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为6元/千克时,每日可售出
为常数.已知销售价格为6元/千克时,每日可售出![]() 系列15千克.
系列15千克.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() 系列的成本为4元/千克,试确定销售价格
系列的成本为4元/千克,试确定销售价格![]() 的值,使该商场每日销售
的值,使该商场每日销售![]() 系列所获得的利润最大.
系列所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是各项均为正整数的等差数列,公差d∈N* , 且{an}中任意两项之和也是该数列中的一项.
(1)若a1=4,则d的取值集合为;
(2)若a1=2m(m∈N*),则d的所有可能取值的和为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com