
分析 (I)根据函数奇偶性的定义即可讨论函数f(x)的奇偶性;
(Ⅱ)求函数的导数,判断函数的单调性和极值,即可作出函数f(x)的图象;
(Ⅲ)根据函数的图象即可求函数f(x)的最大值与最小值.
解答 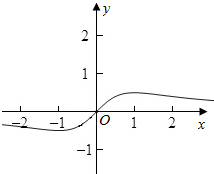 解:(I)函数的定义域为(-∞,+∞),
解:(I)函数的定义域为(-∞,+∞),
则f(-x)=$\frac{-x}{1+{x}^{2}}$=-$\frac{x}{1+{x}^{2}}$=-f(x),
则函数f(x)为奇函数;
(Ⅱ)函数的导数f′(x)=$\frac{1+{x}^{2}-2{x}^{2}}{(1+{x}^{2})^{2}}$=$\frac{1-{x}^{2}}{(1+{x}^{2})^{2}}$,
由f′(x)>0得-1<x<1,此时函数单调递增,
由f′(x)<0得x>1或x<-1,此时函数单调递减,
即当x=1时,函数取得极大值为f(1)=$\frac{1}{2}$,
当x=-1时,函数取得极小值为f(-1)=-$\frac{1}{2}$,
则作出函数f(x)的图象;
(Ⅲ)由图象知,当x=1时,函数取得最大值为f(1)=$\frac{1}{2}$,
当x=-1时,函数取得最小值为f(-1)=-$\frac{1}{2}$.
点评 本题主要考查函数奇偶性和单调性,最值的判断和求解,考查函数的性质.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com