
���� ��1�����˫����$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0���Ľ����߷�����������y2=2px��p��0�����߷��̣��������A��B��������꣬����˫���ߵ�������Ϊ2����AOB�����Ϊ$\sqrt{3}$���г����̣��ɴ˷������p��ֵ��
��2����ֱ��l�ķ��̣����������߷��̣����A��B�����꣬����Τ�ﶨ����ʾ��x1+x2��x1x2�����߶�AB�е������Լ�AB���д��ߵķ��̿ɵã���y=0���뷽�̣�������á�ABEΪ�������Σ����������ǵ������ƶ�E��ֱ��AB�ľ���Ĺ�ϵʽ���k����x0����
��� �⣺��1����˫����$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0����
��˫���ߵĽ����߷�����y=��$\frac{b}{a}$x
��������y2=2px��p��0�����߷�����x=-$\frac{p}{2}$��
��A��B�����������ֱ���y=��$\frac{pb}{2a}$��
����˫���ߵ�������Ϊ2������$\frac{c}{a}$=2����$\frac{b}{a}$=$\sqrt{3}$��
A��B�����������ֱ���y=��$\frac{pb}{2a}$=��$\frac{\sqrt{3}p}{2}$��
�֡�AOB�����Ϊ$\sqrt{3}$��x���ǽ�AOB�Ľ�ƽ����
��$\frac{1}{2}��\sqrt{3}p��\frac{p}{2}$=$\sqrt{3}$����p=2��
��������C�ķ���y2=4x��
��2��������֪��ֱ��l��б�ʴ����Ҳ�Ϊ0�����䷽��Ϊ��y=k��x+1����
����k��0����y2=4x����k2x2+2��k2-2��x+k2=0��
��E��x1��y1����F��x2��y2������x1��x2�Ƿ��̢ٵ�����ʵ��������Τ�ﶨ����x1+x2=-$\frac{2��{k}^{2}-2��}{{k}^{2}}$��x1x2=1
���ԣ��߶�EF���е�����Ϊ��$\frac{2-{k}^{2}}{{k}^{2}}$��$\frac{2}{k}$�����߶�EF�Ĵ�ֱƽ���߷���Ϊy-$\frac{2}{k}$=-$\frac{1}{k}$��x-$\frac{2-{k}^{2}}{{k}^{2}}$����
��y=0��x0=$\frac{2}{{k}^{2}}$+1�����ԣ���P������Ϊ��$\frac{2}{{k}^{2}}$+1��0����
��Ϊ��PEFΪ�������Σ����ԣ���P��$\frac{2}{{k}^{2}}$+1��0����ֱ��EF�ľ������$\frac{\sqrt{3}}{2}$|AB|��
��|EF|=$\frac{4\sqrt{1-{k}^{2}}}{{k}^{2}}•\sqrt{1+{k}^{2}}$��
���ԣ�$\frac{2\sqrt{3}•\sqrt{1-{k}^{2}}}{{k}^{2}}=\frac{2\sqrt{1+{k}^{2}}}{|k|}$���k=$��\frac{\sqrt{3}}{2}$������x0=$\frac{11}{3}$��
���� ���⿼��Բ���ߵĹ�ͬ����������Ĺؼ������˫���ߵĽ����߷��̣����A��B��������꣬�г������ε�����������ʵĹ�ϵҲ�DZ���Ľ���ؼ�����һ����������������ʱҪ�Ͻ��������������


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
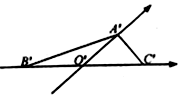 ��֪ˮƽ���õġ�A BC�ǰ���б���⻭�����õ���ͼ��ʾ��ֱ��ͼ������ B'O'=C'O'=1��${A}'{O}'=\frac{{\sqrt{3}}}{2}$����ô����ԭ��ABC���У�������
��֪ˮƽ���õġ�A BC�ǰ���б���⻭�����õ���ͼ��ʾ��ֱ��ͼ������ B'O'=C'O'=1��${A}'{O}'=\frac{{\sqrt{3}}}{2}$����ô����ԭ��ABC���У�������| A�� | AB=BC | B�� | AB=BC����AB��BC | C�� | AB��BC | D�� | AB=AC����AB��AC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16�� | B�� | 12�� | C�� | 8�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com